
【题目】某超市今年 1 月份的销售额为 500 万元,超市预计每个月的销售额会逐月增加.预测 3 月 份的销售额比 2 月份增加 120 万元;
(1)求 2、3 月份平均每月销售额的增长率;
(2)按照这样的增长速度,超市想在第一季度完成 1800 万元的销售目标是否能实现?说明理由.
科目:初中数学 来源: 题型:
【题目】 如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点D是直线AB上一动点(不包含点A,B),过点B作BE⊥CD于点E,连接EA.

(1)如图1,当点D在线段AB上时,直接写出线段CE,BE,AE的数量关系:______.
(2)如图2,当点D在线段AB的延长线上时,判断线段CE,BE,AE的数量关系,并加以证明.
(3)如图3,当点D在线段BA的延长线上时,并将已知条件中的“AB=AC”改成;![]() ,其他条件不变,若CE=1,
,其他条件不变,若CE=1,![]() ,请直接写出线段BE的长.
,请直接写出线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
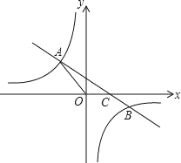
【题目】如图,一次函数y=kx+b(k≠0)的图象与反比例函数![]() 的图象交于二、四象限内的A、B两点,与x轴交于C点,点A的坐标为(﹣2,3),点B的坐标为(4,n).
的图象交于二、四象限内的A、B两点,与x轴交于C点,点A的坐标为(﹣2,3),点B的坐标为(4,n).
(1)求该反比例函数和一次函数的解析式;
(2)在x轴上是否存在点P,使△APC是直角三角形?若存,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
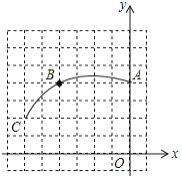
【题目】如图,在正方形网格图中建立平面直角坐标系,一条圆弧经过格点![]() 、
、![]() 、
、![]() ,若该圆弧所在圆的圆心为
,若该圆弧所在圆的圆心为![]() 点,请你利用网格图回答下列问题:
点,请你利用网格图回答下列问题:
(1)圆心![]() 的坐标为_____;
的坐标为_____;
(2)若扇形![]() 是一个圆锥的侧面展开图,求该圆锥底面圆的半径长(结果保留根号).
是一个圆锥的侧面展开图,求该圆锥底面圆的半径长(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第![]() 天(
天(![]() 为整数)的售价、销量及储存和损耗费用的相关信息如表所示.
为整数)的售价、销量及储存和损耗费用的相关信息如表所示.
时间 |
|
|
售价(元/斤) | 第1次降价后的价格 | 第2次降价后的价格 |
销量(斤) |
|
|
储存和损耗费用(元) |
|
|
已知该种水果的进价为4.1元/斤,设销售该水果第![]() (天)的利润为
(天)的利润为![]() (元),求
(元),求![]() 与
与![]() (
(![]() )之间的函数解析式,并求出第几天时销售利润最大.
)之间的函数解析式,并求出第几天时销售利润最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家为支持大学生创业,提供小额无息贷款,学生王芳享受政策无息贷款![]() 元用来代理品牌服装的销售.已知该品牌服装进价每件
元用来代理品牌服装的销售.已知该品牌服装进价每件![]() 元,日销售
元,日销售![]() (件)与销售价
(件)与销售价![]() (元/件)之间的关系如图所示(实线),每天付员工的工资每人每天
(元/件)之间的关系如图所示(实线),每天付员工的工资每人每天![]() 元,每天应支付其它费用
元,每天应支付其它费用![]() 元.
元.

![]() 求日销售
求日销售![]() (件)与销售价
(件)与销售价![]() (元/件)之间的函数关系式;
(元/件)之间的函数关系式;
![]() 若暂不考虑还贷,当某天的销售价为
若暂不考虑还贷,当某天的销售价为![]() 元/件时,收支恰好平衡(收入
元/件时,收支恰好平衡(收入![]() 支出),求该店员工人数;
支出),求该店员工人数;
![]() 若该店只有
若该店只有![]() 名员工,则该店至少需要多少天才能还清贷款,此时,每件服装的价格应定为多少元?
名员工,则该店至少需要多少天才能还清贷款,此时,每件服装的价格应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A,B两点,与y轴交于点C,点O为坐标原点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3,点D为直线AE上方抛物线上的一点
(1)求抛物线所对应的函数解析式;
(2)求△ADE面积的最大值和此时点D的坐标;
(3)将△AOC绕点C逆时针旋转90°,点A对应点为点G,问点G是否在该抛物线上?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
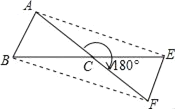
【题目】将△ABC绕点C旋转180°得到△FEC.
(1)试猜想AE与BF有何关系?说明理由.
(2)若△ABC的面积为3cm2,求四边形ABFE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com