
【题目】Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在线段AB上,如图(1)所示,且∠α=50°,则∠1+∠2= °;
(2)若点P在边AB上运动,如图(2)所示,则∠α、∠1、∠2之间的关系为: ;
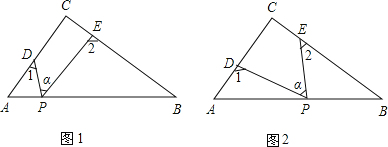
(3)若点P运动到边AB的延长线上,如图(3)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由.
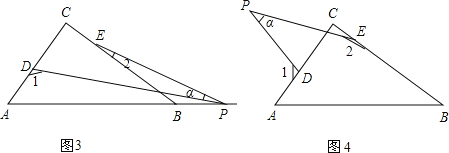
(4)若点P运动到△ABC形外,如图(4)所示,则∠α、∠1、∠2之间的关系为: .
【答案】(1)140°;(2)∠1+∠2=90°+α;(3)∠1=90°+∠2+α,理由见解析;(4)∠2=90°+∠1﹣α.
【解析】试题分析: (1)先用平角的得出,∠CDP=180°-∠1,∠CEP=180°-∠2,最后用四边形的内角和即可;
(2)同(1)方法即可;
(3)利用平角的定义和三角形的内角和即可得出结论;
(4)利用三角形的内角和和外角的性质即可得出结论.
试题解析:
(1)∵∠1+∠2+∠CDP+∠CEP=360°,∠C+∠α+∠CDP+∠CEP=360°,
∴∠1+∠2=∠C+∠α,
∵∠C=90°,∠α=50°,
∴∠1+∠2=140°;
故答案为:140°;
(2)由(1)得出:
∠α+∠C=∠1+∠2,
∴∠1+∠2=90°+α
故答案为:∠1+∠2=90°+α;
(3)∠1=90°+∠2+α,
理由:∵∠2+∠α=∠DME,∠DME+∠C=∠1,
∴∠1=∠C+∠2+α=90°+∠2+α.
(4)∵∠PFD=∠EFC,
∴180°﹣∠PFD=180°﹣∠EFC,
∴∠α+180°﹣∠1=∠C+180°﹣∠2,
∴∠2=90°+∠1﹣α.
故答案为:∠2=90°+∠1﹣α.
点睛:本题考查了三角形内角和定理和外角的性质、对顶角相等的性质,熟练利用三角形外角的性质是解题的关键.


科目:初中数学 来源: 题型:
【题目】我们规定:将一个平面图形分成面积相等的两部分的直线叫做该平面图形的“面线”,“面线”被这个平面图形截得的线段叫做该图形的“面径”(例如圆的直径就是它的“面径”).已知等边三角形的边长为4,则它的“面径”长x的取值范围是 _.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠1=18°18′,∠2=18.18°,∠3=18.3°,下列结论正确的是( )
A. ∠1=∠2 B. ∠1=∠3 C. ∠2=∠3 D. ∠1=∠2=∠3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A的坐标为(3,4),则A关于x轴对称的点的坐标是( )
A. (-3,4) B. (3,-4) C. (-3,-4) D. (4,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)【证法回顾】证明:三角形中位线定理.
已知:如图1,DE是△ABC的中位线.
求证: .
证明:添加辅助线:如图1,在△ABC中,延长DE (D、E分别是AB、AC的中点)到点F,使得EF=DE,连接CF;
请继续完成证明过程:

(2)【问题解决】
如图2,在正方形ABCD中,E为AD的中点,G、F分别为AB、CD边上的点,若AG=2,DF=3,∠GEF=90°,求GF的长.
(3)【拓展研究】
如图3,在四边形ABCD中,∠A=105°,∠D=120°,E为AD的中点,G、F分别为AB、CD边上的点,若AG=![]() ,DF=2,∠GEF=90°,求GF的长.
,DF=2,∠GEF=90°,求GF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com