
【题目】如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.
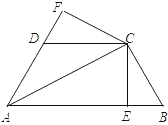
(1)求证:△BCE≌△DCF;
(2)若AB=21,AD=9,BC=CD=10,求AC的长.
【答案】(1)见解析;(2)AC的长为17.
【解析】
(1)首先根据垂线的意义得出∠CFD=∠CEB=90°,然后根据角平分线的性质得出CE=CF,即可判定Rt△BCE≌Rt△DCF;
(2)首先由(1)中全等三角形的性质得出DF=EB,然后判定Rt△AFC≌Rt△AEC,得出AF=AE,构建方程得出CF,再利用勾股定理即可得出AC.
(1)∵AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,
∴∠CFD=90°,∠CEB=90°(垂线的意义)
∴CE=CF(角平分线的性质)
∵BC=CD(已知)
∴Rt△BCE≌Rt△DCF(HL)
(2)由(1)得,
Rt△BCE≌Rt△DCF
∴DF=EB,设DF=EB=x
∵∠CFD=90°,∠CEB=90°,
CE=CF,AC=AC
∴Rt△AFC≌Rt△AEC(HL)
∴AF=AE
即:AD+DF=AB﹣BE
∵AB=21,AD=9,DF=EB=x
∴9+x=21﹣x解得,x=6
在Rt△DCF中,
∵DF=6,CD=10
∴CF=8
∴Rt△AFC中,AC2=CF2+AF2=82+(9+6)2=289
∴AC=17
答:AC的长为17.


科目:初中数学 来源: 题型:
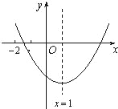
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:
①b2﹣4ac>0;②abc>0;③8a+c>0;④9a+3b+c<0. 其中,正确结论的有_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
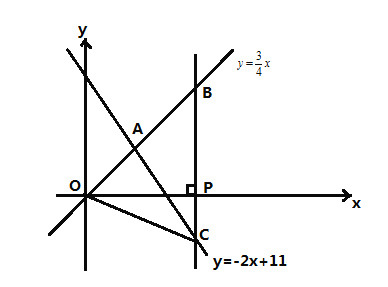
【题目】如图,在平面直角坐标系![]() 中,已知正比例函数
中,已知正比例函数![]() 与一次函数
与一次函数![]() 的图象交于点
的图象交于点![]() ,设
,设![]() 轴上有一点
轴上有一点![]() ,过点
,过点![]() 作
作![]() 轴的垂线(垂线位于点
轴的垂线(垂线位于点![]() 的右侧)分别交
的右侧)分别交![]() 和
和![]() 的图象与点
的图象与点![]() 、
、![]() ,连接
,连接![]() ,若
,若![]() ,则
,则![]() 的面积为( )
的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于E,两线相交于F点.
(1)若∠BAC=60°,∠C=70°,求∠AFB的大小;
(2)若D是BC的中点,∠ABE=30°,求证:△ABC是等边三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,A、B两城市相距100km.现计划在这两座城市间修筑一条高速公路(即线段AB),经测量,森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上.已知森林保护区的范围在以P点为圆心,50km为半径的圆形区域内.请问计划修筑的这条高速公路会不会穿越保护区.为什么?(参考数据:![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
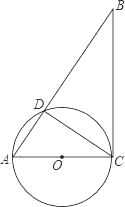
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D点,连接CD.
(1)求证:∠A=∠BCD;
(2)若M为线段BC上一点,试问当点M在什么位置时,直线DM与⊙O相切?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
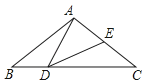
【题目】如图,在△ABC中,点D是边BC上的一点,点E是边AC上的一点,且AB=AC=DC,BD=CE,连接AD、DE.
(1)求证:△ADE是等腰三角形;
(2)若∠ADE=40°,请求出∠BAC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B,C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连结CE.
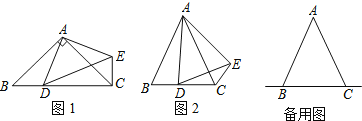
(1)如图1,当点D在线段BC上时,如果∠BAC=90°,则∠BCE= °.
(2)设∠BAC=α,∠BCE=β.
①如图2,当点D在线段BC上移动时,α,β之间有怎样的数量关系?请说明理由.
②当点D在直线BC上移动时,α,β之间有怎样的数量关系?请你在备用图上画出图形,并直接写出你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com