
 2017年南宁市教育局组织全市中小学时候参加安全知识网络竞赛,在安全知识竞赛结束后,赛后发现所有参赛学生会的成绩都高于50分.为了了解本次大赛的成绩分布情况,某校随机抽取了其中200名学生的成绩(成绩x取整数,总分为100分)作为样本进行统计分析,得到如下不完整的统计图表,请根据图标中的信息解答下列各题:
2017年南宁市教育局组织全市中小学时候参加安全知识网络竞赛,在安全知识竞赛结束后,赛后发现所有参赛学生会的成绩都高于50分.为了了解本次大赛的成绩分布情况,某校随机抽取了其中200名学生的成绩(成绩x取整数,总分为100分)作为样本进行统计分析,得到如下不完整的统计图表,请根据图标中的信息解答下列各题:| 成绩(分) | 频数 | 频数 |
| 50<x≤60 | 10 | b |
| 60<x≤70 | 20 | 0.10 |
| 70<x≤80 | 30 | 0.15 |
| 80<x≤90 | a | 0.30 |
| 90<x≤100 | 80 | 0.40 |
分析 (1)根据第二组的频数是20,频率是0.10,求得数据总数,再用数据总数乘以第四组频率可得a的值,用第三组频数除以数据总数可得b的值;根据中位数的定义,将这组数据按照从小到大的顺序排列后,处于中间位置的数据(或中间两数据的平均数)即为中位数;
(2)根据(1)的计算结果即可补全频数分布直方图;
(3)画树状图得出所有等可能的情况数,找出一男一女的情况数,即可求出所求的概率.
解答 解:(1)样本容量是:20÷0.10=200,
a=200×0.30=60,b=10÷200=0.05;
因为一共有200个数据,按照从小到大的顺序排列后,第100个与第101个数据都落在第四个分数段,
所以这次比赛成绩的中位数会落在80≤x<90分数段;
(2)补全频数分布直方图,如下: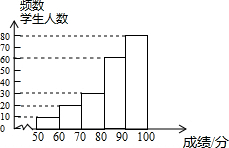
(3)画树状图如下:
所有等可能的情况有12种,其中一男一女有8种,
∴恰好选到一男一女的概率=$\frac{8}{12}$=$\frac{2}{3}$.
故答案为60,0.05;80≤x<90.
点评 本题考查读频数(率)分布直方图的能力和利用统计图获取信息的能力、列表法或树状图法求概率以及条形统计图与扇形统计图;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 类别 | 成绩x分 | 频数(人数) |
| A | 50≤x<60 | 5 |
| B | 60≤x<70 | 7 |
| C | 70≤x<80 | a |
| D | 80≤x<90 | 15 |
| E | 90≤x<100 | 10 |
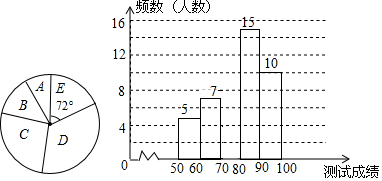
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
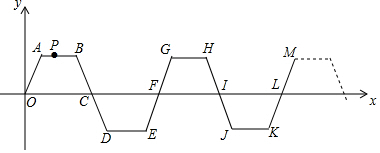
| A. | (1342,0) | B. | (1343,0) | C. | (1344,0) | D. | (1345,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
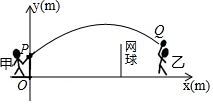 甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x-4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.
甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x-4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.55354×105人 | B. | 5.5354×105人 | C. | 5.5354×104人 | D. | 55.354×103人 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
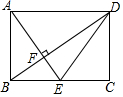 如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,则tan∠BDE的值是( )
如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,则tan∠BDE的值是( )| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{\sqrt{2}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com