

分析 初步体验:根据一组对边平行且相等的四边形是平行四边形得:四边形EBFD是平行四边形,再由平行四边形的对角线互相平分得结论;
规律探究:
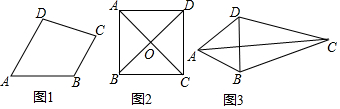
(1)如图2,作辅助线,构建矩形GEFD,利用勾股定理列方程并与矩形的对边相等相结合可得结论;
(2)如图3,同理可得结论;
拓展应用:
如图4,类比如图2,构建矩形GEPD,设BE=EG=x,PD=EG=y,则BP=$\sqrt{2}$x由勾股定理得:BG2+DG2=BD2,则(x+y)2+x2=(4$\sqrt{2}$)2,由已知得:$\sqrt{2}$BP+2PD=4$\sqrt{6}$,则2x+2y=4$\sqrt{6}$ ②,解①和②可得结论.
解答 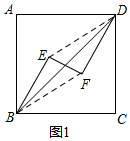 初步体验
初步体验
证明:如图1,连接ED、BF,
∵BE=DF,BE∥DF,
∴四边形EBFD是平行四边形,
∴EF与BD互相平分;
规律探究
(1)如图2,过D作DG⊥BE,交BE的延长线于G,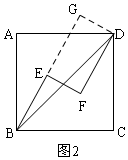
∴∠EGD=∠GEF=∠EFD=90°,
∴四边形GEFD是矩形,
∴EF=GD,EG=DF,
在Rt△BGD中,BG2+DG2=BD2,
∴(BE+EG)2+EF2=BD2,
∵△ABD是等腰直角三角形,
∴BD2=2AB2,
∴(BE+DF)2+EF2=2AB2,
故答案为:2;
(2)不会发生变化,如图3,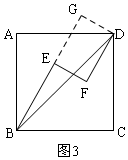 (BE+DF)2+EF2=2AB2仍然成立,
(BE+DF)2+EF2=2AB2仍然成立,
理由是:过D作DG⊥BE,交BE的延长线于G,
∴∠EGD=∠GEF=∠EFD=90°,
∴四边形GEFD是矩形,
∴EF=GD,EG=DF,
在Rt△BGD中,BG2+DG2=BD2,
∴(BE+EG)2+EF2=BD2,
∵△ABD是等腰直角三角形,
∴BD2=2AB2,
∴(BE+DF)2+EF2=2AB2,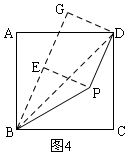
拓展应用
如图4,过P作PE⊥PD,过B作BE⊥PE,过D作DG⊥BE,得矩形GEPD,
∴GD=EP,EG=PD,
设BE=EG=x,PD=EG=y,则BP=$\sqrt{2}$x
∵AB=4,
∴BD=4$\sqrt{2}$,
在Rt△BGD中,由勾股定理得:BG2+DG2=BD2,
∴(x+y)2+x2=(4$\sqrt{2}$)2,
∴2x2+2xy+y2=32 ①,
∵$\sqrt{2}$BP+2PD=4$\sqrt{6}$,
∴2x+2y=4$\sqrt{6}$ ②,
解①和②得:$\left\{\begin{array}{l}{x=2\sqrt{2}}\\{y=2\sqrt{6}-2\sqrt{2}}\end{array}\right.$,
∴PD=2$\sqrt{6}$-2$\sqrt{2}$.
点评 本题是四边形的综合题,考查了平行四边形和矩形的性质和判定,并根据勾股定理列方程解决问题,本题的关键是作辅助线,构建矩形和直角三角形,并运用了类比的思想,使问题得以解决.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
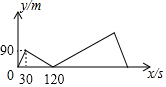 甲、乙两人在1800米长的直线道路上跑步,甲、乙两人同起点、同方向出发,并分别以不同的速度匀速前进.已知,甲出发30秒后,乙出发,乙到终点后立即返回,并以原来的速度前进,最后与甲相遇,此时跑步结束.如图,y(米)表示甲、乙两人之间的距离,t(秒)表示甲出发的时间,图中折线及数据表示整个跑步过程中y与t函数关系.那么,乙到终点后$\frac{360}{7}$秒与甲相遇.
甲、乙两人在1800米长的直线道路上跑步,甲、乙两人同起点、同方向出发,并分别以不同的速度匀速前进.已知,甲出发30秒后,乙出发,乙到终点后立即返回,并以原来的速度前进,最后与甲相遇,此时跑步结束.如图,y(米)表示甲、乙两人之间的距离,t(秒)表示甲出发的时间,图中折线及数据表示整个跑步过程中y与t函数关系.那么,乙到终点后$\frac{360}{7}$秒与甲相遇.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
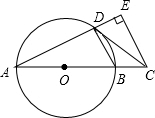 如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.若CE=4,DE=2,则AD的长是( )
如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.若CE=4,DE=2,则AD的长是( )| A. | 2$\sqrt{2}$ | B. | 6 | C. | 3 | D. | 6$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
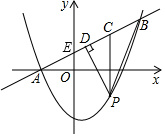 如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+1与y轴交于点E,与抛物线y=ax2+bx-3交于A,B两点,点A在x轴上,点B的纵坐标为3,点P是直线AB下方的抛物线上一动点(不用A,B重合),且点P的横坐标为m,过点P作x轴的垂线交直线AB与点C,作PD⊥AB于点D.
如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+1与y轴交于点E,与抛物线y=ax2+bx-3交于A,B两点,点A在x轴上,点B的纵坐标为3,点P是直线AB下方的抛物线上一动点(不用A,B重合),且点P的横坐标为m,过点P作x轴的垂线交直线AB与点C,作PD⊥AB于点D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
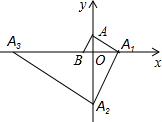 如图,在平面直角坐标系中,点A(0,$\sqrt{3}$)、B(-1,0),过点A作AB的垂线交x轴于点A1,过点A1作AA1的垂线交y轴于点A2,过点A2作A1A2的垂线交x轴于点A3…按此规律继续作下去,直至得到点A2017为止,则点A2017坐标为(31009,0).
如图,在平面直角坐标系中,点A(0,$\sqrt{3}$)、B(-1,0),过点A作AB的垂线交x轴于点A1,过点A1作AA1的垂线交y轴于点A2,过点A2作A1A2的垂线交x轴于点A3…按此规律继续作下去,直至得到点A2017为止,则点A2017坐标为(31009,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com