
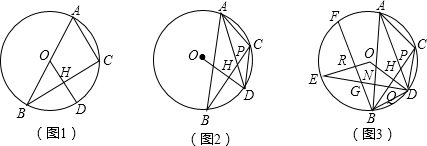
分析 (1)OD⊥BC可知点H是BC的中点,又中位线的性质可得AC=2OH;
(2)由垂径定理可知:$\widehat{BD}=\widehat{CD}$,所以∠BAD=∠CAD,由因为∠ABC=∠ADC,所以∠ACD=∠APB;
(3)由∠ACD-∠ABD=2∠BDN可知∠AND=90°,由tan∠ABC=$\frac{1}{2}$可知NQ和BQ的长度,再由BF⊥OE和OD⊥BC可知∠GBN=∠ABC,所以BG=BQ,连接AO并延长交⊙O于点I,连接IC后利用圆周角定理可求得IC和AI的长度,设QH=x,利用勾股定理可求出QH和HD的长度,利用垂径定理可求得ED的长度,最后利用tan∠OED=$\frac{1}{2}$即可求得RG的长度,最后由垂径定理可求得BF的长度.
解答 解:(1)∵OD⊥BC,
∴由垂径定理可知:点H是BC的中点,
∵点O是AB的中点,
∴OH是△ABC的中位线,
∴AC=2OH;
(2)∵OD⊥BC,
∴由垂径定理可知:$\widehat{BD}=\widehat{CD}$,
∴∠BAD=∠CAD,
∵$\widehat{AC}=\widehat{AC}$,
∴∠ABC=∠ADC,
∴180°-∠BAD-∠ABC=180°-∠CAD-∠ADC,
∴∠ACD=∠APB,
(3)连接AO延长交于⊙O于点I,连接IC,AB与OD相交于点M,
∵∠ACD-∠ABD=2∠BDN,
∴∠ACD-∠BDN=∠ABD+∠BDN,
∵∠ABD+∠BDN=∠AND,
∴∠ACD-∠BDN=∠AND,
∵∠ACD+∠ABD=180°,
∴∠ABD+∠BDN=180°-∠AND,
∴∠AND=180°-∠AND,
∴∠AND=90°,
∵tan∠ABC=$\frac{1}{2}$,BN=3$\sqrt{5}$,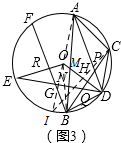
∴NQ=$\frac{3\sqrt{5}}{2}$,
∴由勾股定理可求得:BQ=$\frac{15}{2}$,
∵∠BNQ=∠QHD=90°,
∴∠ABC=∠QDH,
∵OE=OD,
∴∠OED=∠QDH,
∵∠ERG=90°,
∴∠OED=∠GBN,
∴∠GBN=∠ABC,
∵AB⊥ED,
∴BG=BQ=$\frac{15}{2}$,GN=NQ=$\frac{3\sqrt{5}}{2}$,
∵AI是⊙O直径,
∴∠ACI=90°,
∵tan∠AIC=tan∠ABC=$\frac{1}{2}$,
∴$\frac{AC}{IC}$=$\frac{1}{2}$,
∴IC=10$\sqrt{5}$,
∴由勾股定理可求得:AI=25,
连接OB,
设QH=x,
∵tan∠ABC=tan∠ODE=$\frac{1}{2}$,
∴$\frac{QH}{HD}=\frac{1}{2}$,
∴HD=2x,
∴OH=OD-HD=$\frac{25}{2}$-2x,
BH=BQ+QH=$\frac{15}{2}$+x,
由勾股定理可得:OB2=BH2+OH2,
∴($\frac{25}{2}$)2=($\frac{15}{2}$+x)2+($\frac{25}{2}$-2x)2,
解得:x=$\frac{9}{2}$或x=$\frac{5}{2}$,
当QH=$\frac{9}{2}$时,
∴QD=$\sqrt{5}$QH=$\frac{9\sqrt{5}}{2}$,
∴ND=QD+NQ=6$\sqrt{5}$,
∴MN=3$\sqrt{5}$,MD=15
∵MD>$\frac{25}{2}$,
∴QH=$\frac{9}{2}$不符合题意,舍去,
当QH=$\frac{5}{2}$时,
∴QD=$\sqrt{5}$QH=$\frac{5}{2}$$\sqrt{5}$
∴ND=NQ+QD=4$\sqrt{5}$,
由垂径定理可求得:ED=10$\sqrt{5}$,
∴GD=GN+ND=$\frac{11}{2}\sqrt{5}$
∴EG=ED-GD=$\frac{9}{2}$$\sqrt{5}$,
∵tan∠OED=$\frac{1}{2}$,
∴$\frac{RG}{ER}=\frac{1}{2}$,
∴EG=$\sqrt{5}$RG,
∴RG=$\frac{9}{2}$,
∴BR=RG+BG=12
∴由垂径定理可知:BF=2BR=24.
点评 本题考查圆的综合问题,涉及圆周角定理,中位线的性质,锐角三角函数,勾股定理等知识,综合性较强,解答本题需要我们熟练各部分的内容,对学生的综合能力要求较高,一定要注意将所学知识贯穿起来.


科目:初中数学 来源: 题型:解答题
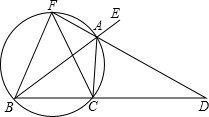 如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB,FC.
如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB,FC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
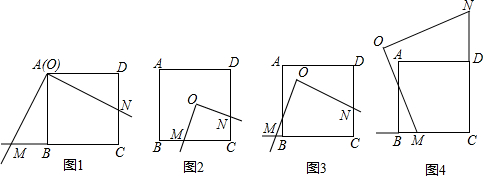
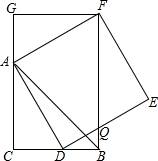 如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:
如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
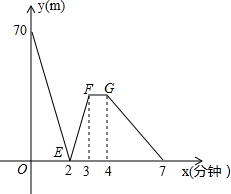 有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,历时7分钟同时到达C点,乙机器人始终以60米/分的速度行走,如图是甲、乙两机器人之间的距离y(米)与他们的行走时间x(分钟)之间的函数图象,请结合图象,回答下列问题:
有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,历时7分钟同时到达C点,乙机器人始终以60米/分的速度行走,如图是甲、乙两机器人之间的距离y(米)与他们的行走时间x(分钟)之间的函数图象,请结合图象,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
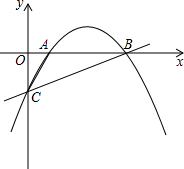 如图,抛物线y=ax2+bx-$\frac{5}{3}$经过点A(1,0)和点B(5,0),与y轴交于点C.
如图,抛物线y=ax2+bx-$\frac{5}{3}$经过点A(1,0)和点B(5,0),与y轴交于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com