
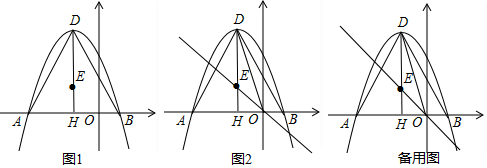
���� ��1����ͼ1�У����������D�Լ���A���꣬���ô���ϵ�������ɽ�����⣮
��2����ͼ2�У����������ٵ�-2-2$\sqrt{3}$��t��-4ʱ���ڵ�-4��t��2$\sqrt{3}$-2ʱ���ֱ���⼴�ɣ�
��3������ͼ3�У�����M��AD��ʱ����EP��OD��P��NK��AD��K��MG��AB��G���ɡ�DPE�ס�OHO��$\frac{ED}{DO}$=$\frac{PE}{OH}$=$\frac{DP}{DH}$�����EP��OP���Ƴ�tan��DOE=tan��ADN=$\frac{EP}{OP}$=$\frac{1}{2}$��
�ɡ�NMK�ա�MHG���Ƴ�NG=MG��MK=HG����AG=a����AM=2a��MG=KN=$\sqrt{3}$a��GH=KM=2$\sqrt{3}$-a��DK=2NK=2$\sqrt{3}$a���ɵ�2a+2$\sqrt{3}$-a+2$\sqrt{3}$a=4$\sqrt{3}$�������M���꣬���ֱ��HM�Ľ���ʽ���ⷽ���������P�ĺ����꣬���ɽ�����⣮����ͼ4�У�����M��BD��ʱ�����ݶԳ��Կ�֪��P�ĺ�����Ϊ1���ɴ˼��ɽ�����⣮
��� �⣺��1����ͼ1�У�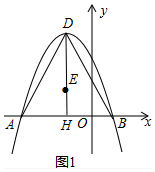
�ߡ�ABD�ǵȱ������Σ�DH��AB��
��AH=BH=2$\sqrt{3}$��
��E��-2��2����
��A��-2-2$\sqrt{3}$��0����B��2$\sqrt{3}$-2��0����
��Rt��ADH�У��ߡ�AHD=90�㣬��ADH=30�㣬
��AD=2AH=4$\sqrt{3}$��DH=$\sqrt{A{D}^{2}-A{H}^{2}}$=6��
��D��-2��6����
�������ߵĽ���ʽΪy=a��x+2��2+6����A��-2-2$\sqrt{3}$��0������õ�a=-$\frac{1}{2}$��
�������ߵĽ���ʽΪy=-$\frac{1}{2}$��x+2��2+6��
��y=-$\frac{1}{2}$x2-2x+4��
��2����ͼ2�У�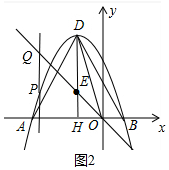
��E��-2��2����
��ֱ��OE�Ľ���ʽΪy=-x����P��t��-$\frac{1}{2}$t2-2t+4������Q��t��-t��
��$\left\{\begin{array}{l}{y=-x}\\{y=-\frac{1}{2}{x}^{2}-2x+4}\end{array}\right.$���$\left\{\begin{array}{l}{x=-4}\\{y=4}\end{array}\right.$��$\left\{\begin{array}{l}{x=2}\\{y=-2}\end{array}\right.$��
�൱-2-2$\sqrt{3}$��t��-4ʱ��d=-t-��-$\frac{1}{2}$t2-2t+4��=$\frac{1}{2}$t2+t-4��
��-4��t��2$\sqrt{3}$-2ʱ��d=��-$\frac{1}{2}$t2-2t+4��-��-t��=-$\frac{1}{2}$t2-t+4��
��3������ͼ3�У�����M��AD��ʱ����EP��OD��P��NK��AD��K��MG��AB��G��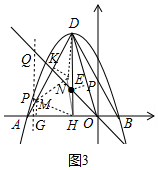
�ɡ�DPE�ס�OHO��$\frac{ED}{DO}$=$\frac{PE}{OH}$=$\frac{DP}{DH}$��
��$\frac{4}{2\sqrt{10}}$=$\frac{PE}{2}$=$\frac{DP}{6}$��
��PE=$\frac{2\sqrt{10}}{5}$��DP=$\frac{6\sqrt{10}}{5}$��
��OP=DO-DP=$\frac{4\sqrt{10}}{5}$��
��tan��DOE=tan��ADN=$\frac{EP}{OP}$=$\frac{1}{2}$��
�ߡ�DPH=��DPN+��NMH=��DAH+��AHP��
�ߡ�NMH=��DAH=60�㣬
���KNM=��MHG��
��MN=MH����NKM=��MGH=90�㣬
���NMK�ա�MHG��
��NG=MG��MK=HG��
��AG=a����AM=2a��MG=KN=$\sqrt{3}$a��GH=KM=2$\sqrt{3}$-a��DK=2NK=2$\sqrt{3}$a��
��2a+2$\sqrt{3}$-a+2$\sqrt{3}$a=4$\sqrt{3}$��
��a=$\frac{12-2\sqrt{3}}{11}$��
��OG=$\frac{24\sqrt{3}+10}{11}$��
���M���꣨-$\frac{24\sqrt{3}+10}{11}$��$\frac{12\sqrt{3}-6}{11}$������H��-2��0����
��ֱ��HM�Ľ���ʽΪy=-$\frac{1}{2}$x-1��
��$\left\{\begin{array}{l}{y=-\frac{1}{2}x-1}\\{y=-\frac{1}{2}{x}^{2}-2x+4}\end{array}\right.$���x=-5��3����������
��t=-5��
��d=$\frac{1}{2}$��25-5-4=$\frac{7}{2}$��
����ͼ4�У�����M��BD��ʱ�����ݶԳ��Կ�֪��P�ĺ�����Ϊ1��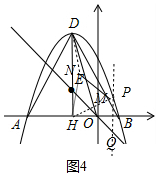
��t=1��
��d=-$\frac{1}{2}$-1+4=$\frac{5}{2}$��
��������������������d��ֵΪ$\frac{7}{2}$��$\frac{5}{2}$��
���� ���⿼����κ����ۺ��⡢����ϵ������������Ǻ�����ȫ�������ε��ж������ʡ����������ε��ж������ʵ�֪ʶ������Ĺؼ������������ѧ֪ʶ��ѧ�����ӳ��ø����߹���ȫ�������λ�ֱ�������Σ�ѧ���÷��̵�˼��˼�����⣬����ؼ����������ͻ�ƿڣ������п�ѹ���⣮


 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д� ������ĩ��ϰ��ѵ��ϵ�д�
������ĩ��ϰ��ѵ��ϵ�д� С��ʿ��ĩ����100��ϵ�д�
С��ʿ��ĩ����100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
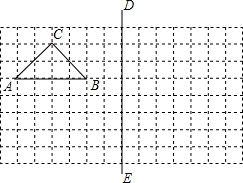 ��ͼ������������ͼ��ÿС���Ϊ�߳���1�������Σ�������¸��⣺����ֱ��ͼ��
��ͼ������������ͼ��ÿС���Ϊ�߳���1�������Σ�������¸��⣺����ֱ��ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
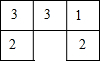 ��ͼ���ɼ����ⳤΪ1��С�������ɵļ�����ĸ���ͼ��С�������е����ֱ�ʾ�ڸ�λ��С������ĸ������뻭����������������ͼ������ͼ�������㴦�ü�����ı������
��ͼ���ɼ����ⳤΪ1��С�������ɵļ�����ĸ���ͼ��С�������е����ֱ�ʾ�ڸ�λ��С������ĸ������뻭����������������ͼ������ͼ�������㴦�ü�����ı�������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ʹ������/h | 500��600 | 600��700 | 700��800 | 800��900 | 900��1000 | 1000��1100 |
| ������/ֻ | 21 | 79 | 108 | 92 | 76 | 24 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
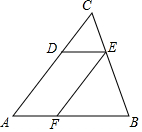 ��ͼ����D��E��F�ֱ��ǡ�ABC�ı�AC��BC��AB�ϵĵ㣬����$\frac{CE}{CB}$=$\frac{CD}{CA}$=$\frac{1}{3}$��$\frac{BF}{BA}$=$\frac{BE}{BC}$=$\frac{2}{3}$������ABC�����Ϊ18cm2ʱ�����ı���AFED�������
��ͼ����D��E��F�ֱ��ǡ�ABC�ı�AC��BC��AB�ϵĵ㣬����$\frac{CE}{CB}$=$\frac{CD}{CA}$=$\frac{1}{3}$��$\frac{BF}{BA}$=$\frac{BE}{BC}$=$\frac{2}{3}$������ABC�����Ϊ18cm2ʱ�����ı���AFED��������鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com