
分析 由x-y=3,y-z=1易得x-z=4,然后把x2+y2+z2-xy-yz+xz进行变形得到$\frac{1}{2}$(2x2+2y2+2z2-2xy-2yz-2xz),根据完全平方公式分组分解为$\frac{1}{2}$[(x-y)2+(y-z)2+(x-z)2],再代值计算即可.
解答 解:∵x-y=3,y-z=1,
∴x-z=4,
∴x2+y2+z2-xy-yz-xz
=$\frac{1}{2}$(2x2+2y2+2z2-2xy-2yz-2xz)
=$\frac{1}{2}$[(x-y)2+(y-z)2+(x-z)2]
=$\frac{1}{2}$(32+12+42)
=$\frac{1}{2}$(9+1+16)
=13.
点评 此题考查因式分解的实际运用,掌握完全平方公式:(a±b)2=a2±2ab+b2是解决问题的关键.


科目:初中数学 来源: 题型:解答题
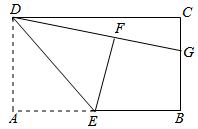 如图,在矩形ABCD中,E是边AB的中点,连接DE,△ADE沿DE折叠后得到△FDE,点F在矩形ABCD的内部,延长DF交于BC于点G.
如图,在矩形ABCD中,E是边AB的中点,连接DE,△ADE沿DE折叠后得到△FDE,点F在矩形ABCD的内部,延长DF交于BC于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
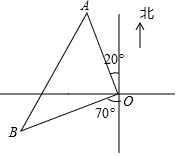 如图,一艘货轮和一艘渔船同时从港口O出发,货轮沿北偏西20°方向航行60海里到达点A处,此时,渔船到达港口O南偏西70°的点B处,与港口O相距80海里,求此时货轮和渔船之间的距离.
如图,一艘货轮和一艘渔船同时从港口O出发,货轮沿北偏西20°方向航行60海里到达点A处,此时,渔船到达港口O南偏西70°的点B处,与港口O相距80海里,求此时货轮和渔船之间的距离.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 选取该校50名女生 | B. | 选取该校50名男生 | ||
| C. | 选取该校一个班级的学生 | D. | 随机选取该校50名学生 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com