练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】坐火车从上海到娄底，高铁G1329次列车比快车K575次列车少需要9小时，已知上海到娄底的铁路长约1260千米，G1329的平均速度是K575的2.5倍．

    （1）求K575的平均速度；

    （2）高铁G1329从上海到娄底只需几小时？

    【答案】（1）84千米/小时；（2）6．

    【解析】试题分析：（1）设K575的平均速度为x千米/小时，根据高铁G1329次列车比快车K575次列车少需要9小时列出分式方程，解方程即可；

    （2）求出G1329的平均速度，计算即可．

    试题解析：解：（1）设K575的平均速度为x千米/小时，则G1329的平均速度是2.5x千米/小时，由题意得： ，解得，x=84．

    答：K575的平均速度为84千米/小时；

    （2）高铁G1329从上海到娄底需要： =6（小时）．

    答：高铁G1329从上海到娄底只需6小时．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，已知平行四边形OABC的三个顶点A、B、C在以O为圆心的半圆上，过点C作CD⊥AB，分别交AB、AO的延长线于点D、E，AE交半圆O于点F，连接CF．

    （1）判断直线DE与半圆O的位置关系，并说明理由；

    （2）①求证：CF=OC；

    ②若半圆O的半径为12，求阴影部分的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：抛物线．

    （1）写出抛物线的开口方向、对称轴；

    （2）函数y有最大值还是最小值？并求出这个最大（小）值；

    （3）设抛物线与y轴的交点为P，与x轴的交点为Q，求直线PQ的函数解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，由正方形ABCD的顶点A引一直线分别交BD、CD及BC的延长线于E、F、G，连接EC.

    求证：CE是△CGF的外接圆⊙O的切线．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线与x轴交于两点A（﹣4，0）和B（1，0），与y轴交于点C（0，2），动点D沿△ABC的边AB以每秒2个单位长度的速度由起点A向终点B运动，过点D作x轴的垂线，交△ABC的另一边于点E，将△ADE沿DE折叠，使点A落在点F处，设点D的运动时间为t秒．

    （1）求抛物线的解析式和对称轴；

    （2）是否存在某一时刻t，使得△EFC为直角三角形？若存在，求出t的值；若不存在，请说明理由；

    （3）设四边形DECO的面积为s，求s关于t的函数表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

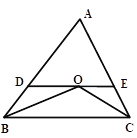
    【题目】如图，∠ABC和∠ACB的平分线交于点O，DE经过点O且平行于BC，分别与AB，AC交于点D、E。

    （1）如图1，若∠ABC=50°，∠ACB=60°，求∠BOC的度数；

    （2）如图1，若∠ABC=α°，∠ACB=β°，用含α、β的式子表示∠BOC的度数；

    （3）探究：如图空白图，在第（2）问的条件下，若∠ABC和∠ACB的邻补角的平分线交于点O，其他条件不变，请画出相应图形，并用含α、β的式子表示∠BOC的度数。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

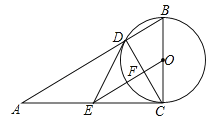
    【题目】如图，在Rt△ABC中，∠ACB=90°，以BC为直径的⊙O交AB于点D，E是AC的中点，OE交CD于点F．

    （1）若∠BCD=36°，BC=10，求 的长；

    （2）判断直线DE与⊙O的位置关系，并说明理由；

    （3）求证： .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】背景资料:

    在已知△ABC所在平面上求一点P，使它到三角形的三个顶点的距离之和最小．

    这个问题是法国数学家费马1640年前后向意大利物理学家托里拆利提出的，所求的点被人们称为“费马点”．

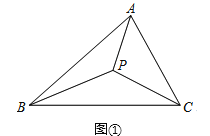
    如图①，当△ABC三个内角均小于120°时，费马点P在△ABC内部，此时∠APB＝∠BPC＝∠CPA＝120°，此时，PA＋PB＋PC的值最小．

    解决问题：

    （1）如图②，等边△ABC内有一点P，若点P到顶点A、B、C的距离分别为3，4，5，求∠APB的度数．

    为了解决本题，我们可以将△ABP绕顶点A旋转到△ACP′处，此时△ACP′≌△ABP，这样就可以利用旋转变换，将三条线段PA，PB，PC转化到一个三角形中，从而求出∠APB=　 　；

    基本运用：

    （2）请你利用第（1）题的解答思想方法，解答下面问题：

    如图③，△ABC中，∠CAB=90°，AB=AC，E，F为BC上的点，且∠EAF=45°，判断BE，EF，FC之间的数量关系并证明；

    能力提升：

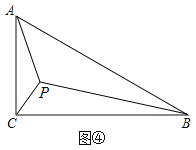
    （3）如图④，在Rt△ABC中，∠C=90°，AC=1，∠ABC=30°，点P为Rt△ABC的费马点，

    连接AP，BP，CP，求PA+PB+PC的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

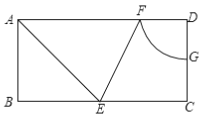
    【题目】如图，矩形ABCD中，BC=2AB=4，AE平分∠BAD交边BC于点E，∠AEC的分线交AD于点F，以点D为圆心，DF为半径画圆弧交边CD于点G，求FG的长.

    查看答案和解析>>

    同步练习册答案