
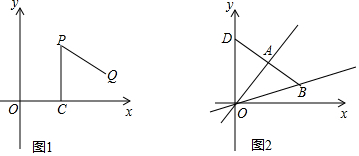
ЗжЮі ЃЈ1ЃЉСЌНгCQПЩжЊЁїPCQЮЊЕШБпШ§НЧаЮЃЌЙ§QзїQDЁЭPCЃЌРћгУЕШБпШ§НЧаЮЕФаджЪПЩЧѓЕУCDКЭQDЕФГЄЃЌдђПЩЧѓЕУQЕузјБъЃЛЩшГіMЕуЕФзјБъЃЌРћгУPЁЂQзјБъжЎМфЕФЙиЯЕПЩЕУЕНЕуMЕФЗНГЬЃЌПЩЧѓЕУMЕуЕФзјБъЃЛ
ЃЈ2ЃЉЂйПЩЩшAЃЈtЃЌ$\frac{\sqrt{3}}{2}$tЃЉЃЌРћгУTБфЛЛПЩЧѓЕУBЕузјБъЃЌРћгУД§ЖЈЯЕЪ§ЪОПЩЧѓЕУжБЯпOBЕФКЏЪ§БэДяЪНЃЛ
ЂкЗНЗЈ1ЁЂгЩД§ЖЈЯЕЪ§ЪОПЩЧѓЕУжБЯпABЕФНтЮіЪНЃЌПЩЧѓЕУDЕузјБъЃЌдђПЩЧѓЕУABЁЂADЕФГЄЃЌПЩЧѓЕУЁїOABЕФУцЛ§гыЁїOADЕФУцЛ§жЎБШЃЎ
ЗНЗЈ2ЁЂЯШШЗЖЈГіЁїBODБШЁїOADЃЈBгыAКсзјБъОјЖджЕЕФБШИќМђЕЅЃЉЕУГіУцЛ§ЙиЯЕЃЌМДПЩЕУГіНсТлЃЎ
НтД№ НтЃК
ЃЈ1ЃЉШчЭМ1ЃЌСЌНгCQЃЌЙ§QзїQDЁЭPCгкЕуDЃЌ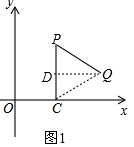
гЩа§зЊЕФаджЪПЩЕУPC=PQЃЌЧвЁЯCPQ=60ЁуЃЌ
ЁрЁїPCQЮЊЕШБпШ§НЧаЮЃЌ
ЁпPЃЈaЃЌbЃЉЃЌ
ЁрOC=aЃЌPC=bЃЌ
ЁрCD=$\frac{1}{2}$PC=$\frac{1}{2}$bЃЌDQ=$\frac{\sqrt{3}}{2}$PQ=$\frac{\sqrt{3}}{2}$bЃЌ
ЁрQЃЈa+$\frac{\sqrt{3}}{2}$bЃЌ$\frac{1}{2}$bЃЉЃЛ
ЩшMЃЈxЃЌyЃЉЃЌдђNЕузјБъЮЊЃЈx+$\frac{\sqrt{3}}{2}$yЃЌ$\frac{1}{2}$yЃЉЃЌ
ЁпNЃЈ6ЃЌ-$\sqrt{3}$ЃЉЃЌ
Ёр$\left\{\begin{array}{l}{x+\frac{\sqrt{3}}{2}y=6}\\{\frac{1}{2}y=-\sqrt{3}}\end{array}\right.$ЃЌНтЕУ$\left\{\begin{array}{l}{x=9}\\{y=-2\sqrt{3}}\end{array}\right.$ЃЌ
ЁрMЃЈ9ЃЌ-2$\sqrt{3}$ЃЉЃЛ
ЙЪД№АИЮЊЃКЃЈa+$\frac{\sqrt{3}}{2}$bЃЌ$\frac{1}{2}$bЃЉЃЛЃЈ9ЃЌ-2$\sqrt{3}$ЃЉЃЛ
ЃЈ2ЃЉЂйЁпAЪЧКЏЪ§y=$\frac{\sqrt{3}}{2}$xЭМЯѓЩЯвьгкдЕуOЕФШЮвтвЛЕуЃЌ
ЁрПЩЩшAЃЈtЃЌ$\frac{\sqrt{3}}{2}$tЃЉЃЌ
Ёрt+$\frac{\sqrt{3}}{2}$ЁС$\frac{\sqrt{3}}{2}$t=$\frac{7}{4}$tЃЌ$\frac{1}{2}$ЁС$\frac{\sqrt{3}}{2}$t=$\frac{\sqrt{3}}{4}$tЃЌ
ЁрBЃЈ$\frac{7}{4}$tЃЌ$\frac{\sqrt{3}}{4}$tЃЉЃЌ
ЩшжБЯпOBЕФКЏЪ§БэДяЪНЮЊy=kxЃЌдђ$\frac{7}{4}$tk=$\frac{\sqrt{3}}{4}$tЃЌНтЕУk=$\frac{\sqrt{3}}{7}$ЃЌ
ЁржБЯпOBЕФКЏЪ§БэДяЪНЮЊy=$\frac{\sqrt{3}}{7}$xЃЛ
ЂкЗНЗЈ1ЁЂЩшжБЯпABНтЮіЪНЮЊy=kЁфx+bЃЌ
АбAЁЂBзјБъДњШыПЩЕУ$\left\{\begin{array}{l}{tkЁф+b=\frac{\sqrt{3}}{2}t}\\{\frac{7}{4}tkЁф+b=\frac{\sqrt{3}}{4}t}\end{array}\right.$ЃЌНтЕУ$\left\{\begin{array}{l}{kЁф=-\frac{\sqrt{3}}{3}}\\{b=\frac{5\sqrt{3}}{6}t}\end{array}\right.$ЃЌ
ЁржБЯпABНтЮіЪНЮЊy=-$\frac{\sqrt{3}}{3}$x+$\frac{5\sqrt{3}}{6}$tЃЌ
ЁрDЃЈ0ЃЌ$\frac{5\sqrt{3}}{6}$tЃЉЃЌЧвAЃЈtЃЌ$\frac{\sqrt{3}}{2}$tЃЉЃЌBЃЈ$\frac{7}{4}$tЃЌ$\frac{\sqrt{3}}{4}$tЃЉЃЌ
ЁрAB=$\sqrt{ЃЈ\frac{7}{4}t-tЃЉ^{2}+ЃЈ\frac{\sqrt{3}}{4}t-\frac{\sqrt{3}}{2}tЃЉ^{2}}$=$\frac{\sqrt{3}}{2}$|t|ЃЌAD=$\sqrt{{t}^{2}+ЃЈ\frac{\sqrt{3}}{2}t-\frac{5\sqrt{3}}{6}tЃЉ^{2}}$=$\frac{2\sqrt{3}}{3}$|t|ЃЌ
Ёр$\frac{{S}_{ЁїOAB}}{{S}_{ЁїOAD}}$=$\frac{AB}{AD}$=$\frac{\frac{\sqrt{3}}{2}|t|}{\frac{2\sqrt{3}}{3}|t|}$=$\frac{3}{4}$ЃЎ
ЗНЗЈ2ЁЂгЩЃЈ1ЃЉжЊЃЌAЃЈtЃЌ$\frac{\sqrt{3}}{2}$tЃЉЃЌBЃЈ$\frac{7}{4}$tЃЌ$\frac{\sqrt{3}}{4}$tЃЉЃЌ
Ёр$\frac{{S}_{ЁїBOD}}{{S}_{ЁїAOD}}=\frac{\frac{1}{2}ODЁС|{x}_{B}|}{\frac{1}{2}ODЁС|{x}_{A}|}$=$\frac{|{x}_{B}|}{|{x}_{A}|}$=$\frac{7}{4}$ЃЌ
ЁпЁїAOBЁЂЁїAODКЭЁїBODЕФБпABЁЂADКЭBDЩЯЕФИпЯрЭЌЃЌ
Ёр$\frac{{S}_{ЁїOAB}}{{S}_{ЁїOAD}}$=$\frac{3}{4}$ЃЎ
ЕуЦР БОЬтЮЊвЛДЮКЏЪ§ЕФзлКЯгІгУЃЌЩцМАЕШБпШ§НЧаЮЕФХаЖЈКЭаджЪЁЂД§ЖЈЯЕЪ§ЗЈЁЂШ§НЧаЮЕФУцЛ§МАЗНГЬЫМЯыЕШжЊЪЖЃЌРэНтЬтФПжаЕФTБфЛЛЪЧНтЬтЕФЙиМќЃЎБОЬтПМВщжЊЪЖЕуНЯЖрЃЌзлКЯадНЯЧПЃЌФбЖШЪЪжаЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | xЁй2 | BЃЎ | xЁн2 | CЃЎ | xЁм2 | DЃЎ | xЃО2 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
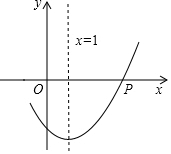 ШчЭМЃЌШєХзЮяЯпy=ax2+bx+cЩЯЕФPЃЈ4ЃЌ0ЃЉЃЌQСНЕуЙигкЫќЕФЖдГЦжсx=1ЖдГЦЃЌдђQЕуЕФзјБъЮЊЃЈ-2ЃЌ0ЃЉЃЎ
ШчЭМЃЌШєХзЮяЯпy=ax2+bx+cЩЯЕФPЃЈ4ЃЌ0ЃЉЃЌQСНЕуЙигкЫќЕФЖдГЦжсx=1ЖдГЦЃЌдђQЕуЕФзјБъЮЊЃЈ-2ЃЌ0ЃЉЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
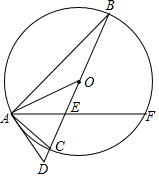 ШчЭМЃЌЁїABCФкНггкЁбOЃЌBCЪЧЁбOЕФжБОЖЃЌЯвAFНЛBCгкЕуEЃЌбгГЄBCЕНЕуDЃЌСЌНгOAЃЌADЃЌЪЙЕУЁЯFAC=ЁЯAODЃЌЁЯD=ЁЯBAFЃЎ
ШчЭМЃЌЁїABCФкНггкЁбOЃЌBCЪЧЁбOЕФжБОЖЃЌЯвAFНЛBCгкЕуEЃЌбгГЄBCЕНЕуDЃЌСЌНгOAЃЌADЃЌЪЙЕУЁЯFAC=ЁЯAODЃЌЁЯD=ЁЯBAFЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
 ШчЭМЃЌШчЙћЁЯDOB+ЁЯBOC=90ЁуЃЌЁЯAOC+ЁЯBOC=90ЁуЃЌФЧУДЁЯDOB=ЁЯAOCЕФРэгЩЪЧЭЌНЧЕФгрНЧЯрЕШЃЎ
ШчЭМЃЌШчЙћЁЯDOB+ЁЯBOC=90ЁуЃЌЁЯAOC+ЁЯBOC=90ЁуЃЌФЧУДЁЯDOB=ЁЯAOCЕФРэгЩЪЧЭЌНЧЕФгрНЧЯрЕШЃЎВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com