


 .
.  的函数图象上,且在第一象限.
的函数图象上,且在第一象限. 轴,垂足为B.
轴,垂足为B.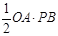 =
= =
= .
.  <12 ;
<12 ; 轴上,不合题意舍去;
轴上,不合题意舍去;  轴,所以点P的横坐标为10,代入
轴,所以点P的横坐标为10,代入  中,
中, ,所以点P坐标(10, 2);
,所以点P坐标(10, 2); . ∴PB 2=" OB·OA" .
. ∴PB 2=" OB·OA" . .
.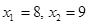 .
.

科目:初中数学 来源:不详 题型:解答题
| 月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 价格y1(元/件) | 560 | 580[ | 600 | 620 | 640 | 660 | 680 | 700 | 720 |

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.(-1,1) | B.(-2,-1) | C.(-3,1) | D.(1,-2) |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的图象与边BC交于点F。
的图象与边BC交于点F。 的值:
的值:
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题


查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.甲的速度是4km/ h | B.乙的速度是10 km/ h |
| C.乙比甲晚出发1 h | D.甲比乙晚到B地3 h |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com