
如图,抛物线y=ax2+bx+c(a≠0)经过点A(-3,0)、B(1,0)、C(-2,1),交y轴于点M.
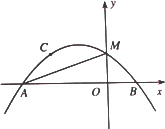
(1)求抛物线的表达式;
(2)D为抛物线在第二象限部分上的一点,作DE垂直x轴于点E,交线段AM于点F,求线段DF长度的最大值,并求此时点D的坐标;
(3)抛物线上是否存在一点P,作PN垂直x轴于点N,使得以点P、A、N为顶点的三角形与△MAO相似?若存在,求点P的坐标;若不存在,请说明理由.
解:由题意可知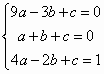 .解得
.解得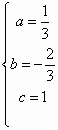 .
.
∴抛物线的表达式为y=![]() .
.
(2)将x=0代入抛物线表达式,得y=1.∴点M的坐标为(0,1).
设直线MA的表达式为y=kx+b,则
![]()
![]() .解得k=
.解得k=![]() ,b=1.∴直线MA的表达式为y=
,b=1.∴直线MA的表达式为y=![]() x+1.
x+1.
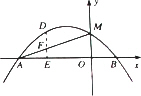
设点D的坐标为(![]() ),则点F的坐标为(
),则点F的坐标为(![]() ).
).
DF=![]()
=![]() .
.
当![]() 时,DF的最大值为
时,DF的最大值为![]() .
.
此时![]() ,即点D的坐标为(
,即点D的坐标为(![]() ).
).
(3)存在点P,使得以点P、A、N为顶点的三角形与△MAO相似.
在Rt△MAO中,AO=3MO,要使两个三角形相似,由题意可知,点P不可能在第一象限.
设点P在第二象限时,∵点P不可能在直线MN上,∴只能PN=3NM,
∴![]() ,即
,即![]() .
.
解得m=-3(舍去)或m=-8.又-3<M<0,故此时满足条件的点不存在.
当点P在第三象限时,∵点P不可能在直线MN上,∴只能PN=3NM,
∴![]() ,即
,即![]() .
.
解得m=-3或m=8.此时点P的坐标为(-8,,15).
当点P在第四象限时,

若AN=3PN时,则-3![]() ,即
,即![]() .
.
解得m=-3(舍去)或m=2.
当m=2时,![]() .此时点P的坐标为(2,-
.此时点P的坐标为(2,-![]() ).
).
若PN=3NA,则-![]() ,即
,即![]() .
.
解得m=-3(舍去)或m=10,此时点P的坐标为(10,,39).
综上所述,满足条件的点P的坐标为(-8,,15)、(2,-![]() )、(10,,39).
)、(10,,39).


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源:2008年江西省南昌市初中毕业升学统一考试、数学试卷 题型:044
如图,抛物线y1=-ax2-ax+1经过点P![]() ,且与抛物线y2=ax2-ax-1,相交于A,B两点.
,且与抛物线y2=ax2-ax-1,相交于A,B两点.
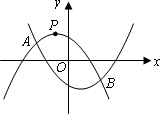
(1)求a值;
(2)设y1=-ax2-ax+1与x轴分别交于M,N两点(点M在点N的左边),y2=ax2-ax-1与x轴分别交于E,F两点(点E在点F的左边),观察M,N,E,F四点的坐标,写出一条正确的结论,并通过计算说明;
(3)设A,B两点的横坐标分别记为xA,xB,若在x轴上有一动点Q(x,0),且xA≤≤x≤xB,过Q作一条垂直于x轴的直线,与两条抛物线分别交于C,D两点,试问当x为何值时,线段CD有最大值?其最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
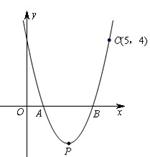
(本题满分8分)如图,抛物线y=ax-5x+4a与x轴相交于点A、B,且经过点C(5,4).该抛物线顶点为P.

1.⑴求a的值和该抛物线顶点P的坐标.
2.⑵求DPAB的面积;
3.⑶若将该抛物线先向左平移4个单位,再向上平移2个单位,求出平移后抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2012届江苏省兴化市九年级上学期期末四校联考数学卷 题型:解答题
(本题满分8分)如图,抛物线y=ax-5x+4a与x轴相交于点A、B,且经过点C(5,4).该抛物线顶点为P.
【小题1】⑴求a的值和该抛物线顶点P的坐标.
【小题2】⑵求DPAB的面积;
【小题3】⑶若将该抛物线先向左平移4个单位,再向上平移2个单位,求出平移后抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省兴化市九年级上学期期末四校联考数学卷 题型:解答题
(本题满分8分)如图,抛物线y=ax-5x+4a与x轴相交于点A、B,且经过点C(5,4).该抛物线顶点为P.
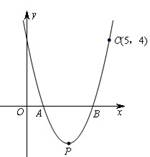
1.⑴求a的值和该抛物线顶点P的坐标.
2.⑵求DPAB的面积;
3.⑶若将该抛物线先向左平移4个单位,再向上平移2个单位,求出平移后抛物线的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com