
【题目】如图,抛物线 ![]() 与
与 ![]() 轴交于
轴交于 ![]() 、
、 ![]() 两点(点
两点(点 ![]() 在点
在点 ![]() 的左侧),点
的左侧),点 ![]() 的坐标为
的坐标为 ![]() ,与
,与 ![]() 轴交于点
轴交于点 ![]() ,作直线
,作直线 ![]() .动点
.动点 ![]() 在
在 ![]() 轴上运动,过点
轴上运动,过点 ![]() 作
作 ![]() 轴,交抛物线于点
轴,交抛物线于点 ![]() ,交直线
,交直线 ![]() 于点
于点 ![]() ,设点
,设点 ![]() 的横坐标为
的横坐标为 ![]() .
.
(Ⅰ)求抛物线的解析式和直线 ![]() 的解析式;
的解析式;
(Ⅱ)当点 ![]() 在线段
在线段 ![]() 上运动时,求线段
上运动时,求线段 ![]() 的最大值;
的最大值;
(Ⅲ)当以 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 为顶点的四边形是平行四边形时,直接写出
为顶点的四边形是平行四边形时,直接写出 ![]() 的值.
的值.
【答案】解:(I)∵抛物线过A、C两点,
∴代入抛物线解析式可得 ![]() ,解得
,解得 ![]() ,
,
∴抛物线解析式为y=﹣x2+2x+3,
令y=0可得,﹣x2+2x+3=0,解x1=﹣1,x2=3,
∵B点在A点右侧,
∴B点坐标为(3,0),
设直线BC解析式为y=kx+s,
把B、C坐标代入可得 ![]() ,解得
,解得 ![]() ,
,
∴直线BC解析式为y=﹣x+3;
(Ⅱ)∵PM⊥x轴,点P的横坐标为m,
∴M(m,﹣m2+2m+3),N(m,- m+3),
∵P在线段OB上运动,
∴M点在N点上方,
∴MN=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m=﹣(m﹣ ![]() )2+
)2+ ![]() ,
,
∴当m= ![]() 时,MN有最大值,MN的最大值为
时,MN有最大值,MN的最大值为 ![]() ;
;
(Ⅲ)∵PM⊥x轴,
∴MN∥OC,
当以C、O、M、N为顶点的四边形是平行四边形时,则有OC=MN,
当点P在线段OB上时,则有MN=﹣m2+3m,
∴﹣m2+3m=3,此方程无实数根,
当点P不在线段OB上时,则有MN=﹣m+3﹣(﹣m2+2m+3)=m2﹣3m,
∴m2﹣3m=3,解得m= ![]() 或m=
或m= ![]() ,
,
综上可知当以C、O、M、N为顶点的四边形是平行四边形时,m的值为 ![]() 或
或 ![]()
【解析】(Ⅰ)利用待定系数法可求出抛物线的解析式和直线BC解析式;
(Ⅱ)点P的横坐标为m,根据题意可用m表示出M、N的坐标,从而得出MN与m的函数关系式,再化成顶点式可求其最值;
(Ⅲ)当以C、O、M、N为顶点的四边形是平行四边形时,则有OC=MN,且OC∥MN,可得MN=﹣m+3﹣(﹣m2+2m+3)=m2﹣3m,即m2﹣3m=3,从而求出m的值.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y= ![]() (x>0)的图象交于A(m,6),B(3,n)两点,与x轴交于点C,与y轴交于点D,下列结论:①一次函数解析式为y=﹣2x+8;②AD=BC;③kx+b﹣
(x>0)的图象交于A(m,6),B(3,n)两点,与x轴交于点C,与y轴交于点D,下列结论:①一次函数解析式为y=﹣2x+8;②AD=BC;③kx+b﹣ ![]() <0的解集为0<x<1或x>3;④△AOB的面积是8,其中正确结论的个数是( )
<0的解集为0<x<1或x>3;④△AOB的面积是8,其中正确结论的个数是( )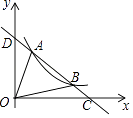
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2AD,点E,F分别是AB,BC边的中点,连接AF,CE交于点M,连接BM并延长交CD于点N,连接DE交AF于点P,则结论:①∠ABN=∠CBN;②DE∥BN;③△CDE是等腰三角形;④EM:BE= ![]() :3;⑤S△EPM=
:3;⑤S△EPM= ![]() S梯形ABCD , 正确的个数有( )
S梯形ABCD , 正确的个数有( )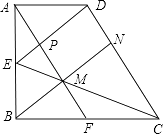
A.5个
B.4个
C.3个
D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点C(﹣3,0),点A,B分别在x轴,y轴的正半轴上,且满足 ![]() +|OA﹣1|=0
+|OA﹣1|=0
(1)求点A,点B的坐标.
(2)若点P从C点出发,以每秒1个单位的速度沿射线CB运动,连结AP.设△ABP的面积为S,点P的运动时间为t秒,求S与t的函数关系式,并写出自变量的取值范围.
(3)在(2)的条件下,是否存在点P,使以点A,B,P为顶点的三角形与△AOB相似?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小宇家附近新修了一段公路,他想给市政写信,建议在路的两边种上银杏树![]() 他先让爸爸开车驶过这段公路,发现速度为60千米
他先让爸爸开车驶过这段公路,发现速度为60千米![]() 小时,走了约3分钟,由此估算这段路长约______千米.
小时,走了约3分钟,由此估算这段路长约______千米.
然后小宇查阅资料,得知银杏为落叶大乔木,成年银杏树树冠直径可达8米![]() 小宇计划从路的起点开始,每隔a米种一棵树,绘制示意图如图:
小宇计划从路的起点开始,每隔a米种一棵树,绘制示意图如图:
考虑到投入资金的限制,他设计了另一种方案,将原计划的a扩大一倍,则路的两侧共计减少200棵数,请你求出a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线 ![]() 的对称轴为直线
的对称轴为直线 ![]() ,与
,与 ![]() 轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:
轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论: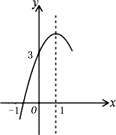
① ![]() ;② 方程
;② 方程 ![]() 的两个根是
的两个根是 ![]() ;③
;③ ![]() ;④当
;④当 ![]() 时,
时, ![]() 的取值范围是
的取值范围是 ![]() ;⑤ 当
;⑤ 当 ![]() 时,
时, ![]() 随
随 ![]() 增大而增大;其中结论正确有.
增大而增大;其中结论正确有.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如下表:
原进价 | 零售价 | |
餐桌 | a | 270 |
餐椅 | b | 70 |
若购进4张餐桌19张餐椅需要1360元;若购进6张餐桌26张餐椅需要1940元.
![]() 求表中a,b的值;
求表中a,b的值;
![]() 今年年初由于原材料价格上涨,每张餐桌的进价上涨了10元,每张餐椅的进价上涨了
今年年初由于原材料价格上涨,每张餐桌的进价上涨了10元,每张餐椅的进价上涨了![]() ,商场决定购进餐桌30张,餐椅170张进行销售,全部售出后,要求利润不低于7380元,求m的最大值.
,商场决定购进餐桌30张,餐椅170张进行销售,全部售出后,要求利润不低于7380元,求m的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com