
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是边
是边![]() 的中点,以
的中点,以![]() 为腰向外作等腰直角三角形
为腰向外作等腰直角三角形![]() ,
,![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)若![]() ,则
,则![]() ;
;
(2)求证: ![]() ;
;
(3)若![]() ,则
,则![]() .
.

【答案】(1) 20°; (2)见解析;(3)18.
【解析】
(1)根据等腰直角三角形的旋转得出∠ABE=∠AEB,求出∠BAE,根据三角形内角和定理求出即可;
(2)根据等腰三角形的性质得出∠BAF=∠CAF,根据SAS推出△BAF≌△CAF,根据全等得出∠ABF=∠ACF,即可得出答案;
(3)根据全等得出BF=CF,求出∠CFG=∠EAG=90°,根据勾股定理求出EF2+BF2=EF2+CF2=EC2,EC2=AC2+AE2=2AC2,即可得出答案.
(1)∵AB=AC,△ACE是等腰直角三角形,
∴AB=AE,
∴∠ABE=∠AEB,
又∵∠BAC=50°,∠EAC=90°,
∴∠BAE=50°+90°=140°,
∴∠AEB=(180°140°)÷2=20°;
(2)证明:∵AB=AC,D是BC的中点,
∴∠BAF=∠CAF.
在△BAF和△CAF中, ![]() ,
,
∴△BAF≌△CAF(SAS).
∴∠ABF=∠ACF.
又∵AB=AC,
∴∠ABE=∠AEB,
∴∠AEB=∠ACF.
(3)
∵△BAF≌△CAF,
∴BF=CF.
∴∠AEB=∠ACF,∠AGE=∠FGC.
∴∠CFG=∠EAG=90°.
∴EF2+BF2=EF2+CF2=EC2.
∵△ACE是等腰直角三角形,
∴∠CAE=90°,AC=AE.
∴EC2=AC2+AE2=2AC2=18.
即EF2+BF2=18.
故答案为:18.


科目:初中数学 来源: 题型:
【题目】在甲、乙两名同学中选拔一人参加“中华好诗词”大赛,在相同的测试条件下,两人5次测试成绩(单位:分)如下:
甲:79,86,82,85,83
乙:88,79,90,81,72.
回答下列问题:
(1)甲成绩的平均数是______ ,乙成绩的平均数是______ ;
(2)经计算知S甲2=6,S乙2=42.你认为选拔谁参加比赛更合适,说明理由;
(3)如果从甲、乙两人5次的成绩中各随机抽取一次成绩进行分析,求抽到的两个人的成绩都大于80分的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在长方形![]() 中,
中,![]() cm,
cm,![]() cm.现将其按下列步骤折叠:(1)将边
cm.现将其按下列步骤折叠:(1)将边![]() 向边
向边![]() 折叠,使边
折叠,使边![]() 落在边
落在边![]() 上,得到折痕
上,得到折痕![]() ,如图②;(2)将
,如图②;(2)将![]() 沿
沿![]() 折叠,
折叠,![]() 与
与![]() 交于点
交于点![]() ,如图③.则所得梯形
,如图③.则所得梯形![]() 的周长等于( )
的周长等于( )
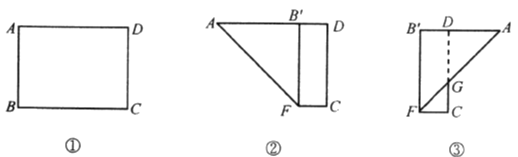
A. ![]() cm B.
cm B. ![]() cm
cm
C. ![]() cm D.
cm D. ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE,点B经过的路径为 , 则图中阴影部分的面积是 . 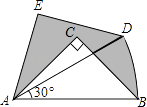
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△EBD中,∠ABC=∠DBE=90°,AB=CB,BE=BD,连接AE,CD,AE与CD交于点M,AE与BC交于点N.
(1)求证:AE=CD;
(2)求证:AE⊥CD;
(3)连接BM,有以下两个结论:①BM平分∠CBE;②MB平分∠AMD.其中正确的有 (请写序号,少选、错选均不得分).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解下列方程时,配方正确的是( )
A.方程x2﹣6x﹣5=0,可化为(x﹣3)2=4
B.方程y2﹣2y﹣2015=0,可化为(y﹣1)2=2015
C.方程a2+8a+9=0,可化为(a+4)2=25
D.方程2x2﹣6x﹣7=0,可化为 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在下列条件中,不能作为判断△ABD≌△BAC的条件是( )

A. ∠D=∠C,∠BAD=∠ABC B. ∠BAD=∠ABC,∠ABD=∠BAC
C. BD=AC,∠BAD=∠ABC D. AD=BC,BD=AC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com