

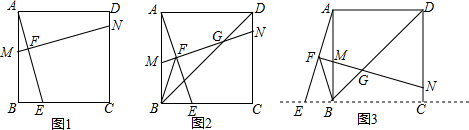
���� ��1���跨֤����BAD�ա�CAF���FCD=90�㼴�ɣ�
��2���루1��ͬ����
��3���еĢ��루1����ͬ����֤��BD=CF���ֵ�D��B��C���ߣ��ʣ�CD=BC+CF��
���ɣ�1�����벢֤��BD��CF���Ӷ���֪��FCDΪֱ�������Σ����������εĶԽ��ߵ������ж���AOC���ߵ��ص㣬�ٽ�һ���ж�����״��
��� ��1��֤�����ߡ�BAC=90�㣬AB=AC��
���ABC=��ACB=45�㣬
���ı���ADEF�������Σ�
��AD=AF����DAF=90�㣬
�ߡ�BAC=��BAD+��DAC=90�㣬��DAF=��CAF+��DAC=90�㣬
���BAD=��CAF��
�ڡ�BAD�͡�CAF�У�
$\left\{\begin{array}{l}{AB=AC}\\{��BAD=��CAF}\\{AD=AF}\end{array}\right.$��
���BAD�ա�CAF��SAS����
��BD=CF����ACF=��ABD=45�㣬
���ACF+��ACB=90�㣬
��BD��CF��
��2����1���Ľ�����Ȼ���������ɣ�
�ߡ�BAD=��BAC+��CAD=90��+��CAD��
��CAF=��DAF+��CAD=90��+��CAD��
���BAD=��CAF��
�ڡ�BAD�͡�CAF�У�
$\left\{\begin{array}{l}{AB=AC}\\{��BAD=��CAF}\\{AD=AF}\end{array}\right.$
���BAD�ա�CAF��SAS����
��BD=CF����ACF=��ABD=45��
���BCF=��ACB+��ACF=45��+45��=90��
��BD��CF��
��3����BC��CD��CF�Ĺ�ϵ��CD=BC+CF
���ɣ��루1��ͬ����֤��BAD�ա�CAF���Ӷ��ɵã�
BD=CF��
����CD=BC+CF
�ڡ�AOC�ǵ���������
���ɣ��루1��ͬ����֤��BAD�ա�CAF���ɵã���DBA=��FCA��
�֡ߡ�BAC=90�㣬AB=AC��
���ABC=��ACB=45�㣬
���ABD=180��-45��=135�㣬
���ABD=��FCA=135��
���DCF=135��-45��=90��
���FCDΪֱ�������Σ�
�֡��ı���ADEF�������Σ��Խ���AE��DF�ཻ�ڵ�O��
��OC=$\frac{1}{2}$DF��
��OC=OA
���AOC�ǵ��������Σ�
���� ���⿼���˵��������Ρ������ε����ʼ�ȫ�������ε��ж������ʵ�֪ʶ�㣬һ������£�Ҫ֤�������߶���ȣ��͵�֤���������߶����ڵ�����������ȫ�ȣ��ؼ�������ͼ���ص��ھ���Ŀ��������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 4x-4 | C�� | 4-4x | D�� | 4+4x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ھ���ABCD�У�AD=$\sqrt{2}$AB����BAD��ƽ���߽�BC�ڵ�E��DH��AE�ڵ�H������BH���ӳ���CD�ڵ�F������DE��BF�ڵ�O�����н��ۣ�
��ͼ���ھ���ABCD�У�AD=$\sqrt{2}$AB����BAD��ƽ���߽�BC�ڵ�E��DH��AE�ڵ�H������BH���ӳ���CD�ڵ�F������DE��BF�ڵ�O�����н��ۣ�| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com