【题目】甲班56人，其中身高在160厘米以上的男同学10人，身高在160厘米以上的女同学3人，乙班80人，其中身高在160厘米以上的男同学20人，身高在160厘米以上的女同学8人．如果想在两个班的160厘米以上的女生中抽出一个作为旗手，在哪个班成功的机会大？为什么？
七彩题卡口算应用一点通系列答案科目：初中数学 来源： 题型：
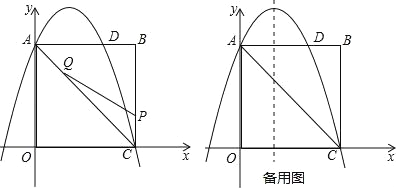
【题目】如图，在矩形OABC中，点O为原点，点A的坐标为（0，8），点C的坐标为（6，0）．抛物线y＝﹣
x2+bx+c经过点A、C，与AB交于点D．
（1）求抛物线的函数解析式；
（2）点P为线段BC上一个动点（不与点C重合），点Q为线段AC上一个动点，AQ＝CP，连接PQ，设CP＝m，△CPQ的面积为S．
①求S关于m的函数表达式；
②当S最大时，在抛物线y＝﹣x2+bx+c的对称轴l上，若存在点F，使△DFQ为直角三角形，请直接写出所有符合条件的点F的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知：E是∠AOB的平分线上一点，EC⊥OB，ED⊥OA，C、D是垂足，连接CD，且交OE于点F.
（1）求证：OE是CD的垂直平分线.
（2）若∠AOB=60，请你探究OE，EF之间有什么数量关系？并证明你的结论。
查看答案和解析>>
科目：初中数学 来源： 题型：
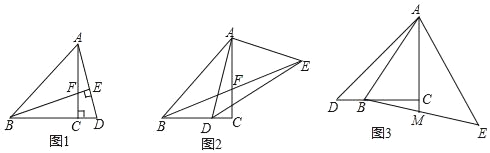
【题目】已知：△ABC中，∠ACB＝90°，AC＝BC．
（1）如图1，点D在BC的延长线上，连AD，过B作BE⊥AD于E，交AC于点F．求证：AD＝BF；
（2）如图2，点D在线段BC上，连AD，过A作AE⊥AD，且AE＝AD，连BE交AC于F，连DE，问BD与CF有何数量关系，并加以证明；
（3）如图3，点D在CB延长线上，AE＝AD且AE⊥AD，连接BE、AC的延长线交BE于点M，若AC＝3MC，请直接写出
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
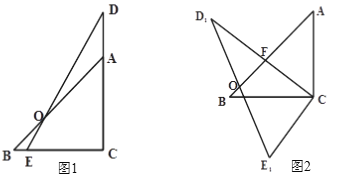
【题目】把两个直角三角形如图(1)放置,使∠ACB与∠DCE重合,AB与DE相交于点O,其中∠DCE=90°,∠BAC=45°,AB=6
cm,CE=5cm, CD=10cm．
(1)图1中线段AO的长= cm；DO=cm
(2)如图2,把△DCE绕着点C逆时针旋转α度（0°＜α＜90°）得△D1CE1,D1C与AB相交于点F,若△BCE1恰好是以BC为底边的等腰三角形,求线段AF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】有一直角三角形两直角边分别为6
、8，在其外部拼上一个以8为直角边的直角三角形，此时变成等腰三角形，则该等腰三角形的周长是__________．
查看答案和解析>>
科目：初中数学 来源： 题型：
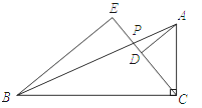
【题目】已知：如图，Rt△ABC中，∠ACB=90°，P是边AB上一点，AD⊥CP，BE⊥CP，垂足分别为D、E，已知AB=3
，BC=3
，BE=5．求DE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】自2016年国庆后，许多高校均投放了使用手机就可随用的共享单车．某运营商为提高其经营的A品牌共享单车的市场占有率，准备对收费作如下调整：一天中，同一个人第一次使用的车费按0.5元收取，每增加一次，当次车费就比上次车费减少0.1元，第6次开始，当次用车免费．具体收费标准如下：
使用次数 | 0 | 1 | 2 | 3 | 4 | 5(含5次以上) |
累计车费 | 0 | 0.5 | 0.9 |
|
| 1.5 |
同时，就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿，得到如下数据：
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 5 | 15 | 10 | 30 | 25 | 15 |
（Ⅰ）写出
的值；
（Ⅱ）已知该校有5000名师生，且A品牌共享单车投放该校一天的费用为5800元．试估计：收费调整后，此运营商在该校投放A品牌共享单车能否获利? 说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
