
【题目】如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4,
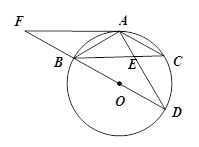
(1)求证:△ABE∽△ADB;
(2)求AB的长;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.
【答案】

【解析】试题分析:(1)根据AB=AC,可得∠ABC=∠C,利用等量代换可得∠ABC=∠D然后即可证明△ABE∽△ADB.
(2)根据△ABE∽△ADB,利用其对应边成比例,将已知数值代入即可求得AB的长.
(3)连接OA,根据BD为⊙O的直径可得∠BAD=90°,利用勾股定理求得BD,然后再求证∠OAF=90°即可.
(1)证明:∵AB=AC,
∴∠ABC=∠C(等边对等角),
∵∠C=∠D(同弧所对的圆周角相等),
∴∠ABC=∠D(等量代换),
又∵∠BAE=∠DAB,
∴△ABE∽△ADB,
(2)解:∵△ABE∽△ADB,
∴![]() ,
,
∴AB2=ADAE=(AE+ED)AE=(2+4)×2=12,
∴AB=.
(3)解:直线FA与⊙O相切,理由如下:
连接OA,∵BD为⊙O的直径,
∴∠BAD=90°,
∴![]() =4
=4
BF=BO=![]() ,
,
∵AB=,
∴BF=BO=AB,
∴∠OAF=90°,
∴OA⊥AF,
∵AO是圆的半径,
∴直线FA与⊙O相切.


科目:初中数学 来源: 题型:
【题目】如图,点A,B为定点,定直线l//AB,P是l上一动点.点M,N分别为PA,PB的中点,对于下列各值:①线段MN的长;②△PMN的面积;③△PAB的周长;④∠APB的大小;⑤直线MN,AB之间的距离.其中会随点P的移动而不改变的是( )

A. ①②③ B. ①②⑤ C. ②③④ D. ②④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
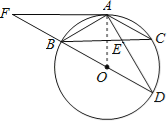
【题目】已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C、D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆心O到直线AB的距离为6,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分6分)
(1)(3分)(-3)2-|-![]() |+(3.14-x)0
|+(3.14-x)0
(2)(4分)先化简,再求值:[(2x-y)2+(2x-y)(2x+y)]÷(4x),其中x=2,y=-1
查看答案和解析>>
科目:初中数学 来源: 题型:
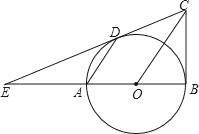
【题目】如图所示,已知AB是⊙O的直径,BC⊥AB,连接OC,弦AD∥OC,直线CD交BA的延长线于点E.
(1)求证:直线CD是⊙O的切线;
(2)若DE=2BC,求AD:OC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图AB∥CD,点P是平面内直线AB、CD外一点连接PA、PC。
(1)写出所给的四个图形中∠APC、∠PAB、∠PCD之间的数量关系;
(2)证明图(1)和图(3)的结论。

查看答案和解析>>
科目:初中数学 来源: 题型:
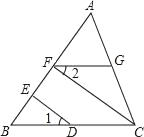
【题目】如图所示,∠1=∠2,CF⊥AB,DE⊥AB,垂足分别为点F、E,求证:FG∥BC.
证明:∵CF⊥AB、DE⊥AB(已知)
∴∠BED=90°、∠BFC=90°
∴∠BED=∠BFC
∴( )∥( )( )
∴∠1=∠BCF( )
又∵∠1=∠2(已知)
∴∠2=∠BCF( )
∴FG∥BC( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 于点
于点![]()
(1)如图1,若![]() 的角平分线交
的角平分线交![]() 于点
于点![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(2)如图2,点![]() 分别在线段
分别在线段![]() 上,将
上,将![]() 折叠,点
折叠,点![]() 落在点
落在点![]() 处,点
处,点![]() 落在点
落在点![]() 处,折痕分别为
处,折痕分别为![]() 和
和![]() ,且点
,且点![]() ,点
,点![]() 均在直线
均在直线![]() 上,若
上,若![]() ,试猜想
,试猜想![]() 与
与![]() 之间的数量关系,并加以证明;
之间的数量关系,并加以证明;
(3)在(2)小题的条件下,将![]() 绕点
绕点![]() 逆时针旋转一个角度
逆时针旋转一个角度![]() (
(![]() ),记旋转中的
),记旋转中的![]() 为
为![]() (如图3),在旋转过程中,直线
(如图3),在旋转过程中,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,若
,若![]() ,是否存在这样的
,是否存在这样的![]() 两点,使
两点,使![]() 为直角三角形?若存在,请直接写出旋转角
为直角三角形?若存在,请直接写出旋转角![]() 的度数;若不存在,请说明理由.
的度数;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com