
 如图,已知抛物线y=ax2-x+c的对称轴为直线x=1,与x轴的一个交点为A(-1,0),顶点为B,点C(5,m)在抛物线上,直线BC交x轴于点E.
如图,已知抛物线y=ax2-x+c的对称轴为直线x=1,与x轴的一个交点为A(-1,0),顶点为B,点C(5,m)在抛物线上,直线BC交x轴于点E.分析 (1)先利用待定系数法求抛物线解析式,进而求出点B,C坐标,求出直线BC解析式即可得出结论;
(2)先判断出△ABC是直角三角形,即可得出结论;
(3)先判断出∠CGM=∠B,再分两种情况建立方程求解即可.
解答 解:(1)∵抛物线y=ax2-x+c的对称轴为直线x=1,与x轴的一个交点为A(-1,0),
∴$\left\{\begin{array}{l}{-\frac{-1}{2a}=1}\\{a+1+c=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{c=-\frac{3}{2}}\end{array}\right.$,
∴抛物线的表达式为y=$\frac{1}{2}$x2-x-$\frac{3}{2}$;
∴顶点B(1,-2),点C(5,6),
∴直线BC的解析式为y=2x-4,
∵直线BC交x轴于点E,
∴E(2,0);
(2)∵A(-2,0),B(1,2),C(5,6),
∴AB2=(-1-1)2+22=8,AC2=(-1-5)2+62=72,BC2=(5-1)2+(6+2)2=80,
∴AB2+AC2=BC2,
∴∠BAC=90°,
∴tan∠B=$\frac{AC}{AB}$=$\frac{6\sqrt{2}}{2\sqrt{2}}$=3;
(3)∵∠CAB=90°,
∴∠B+∠ACB=90°.
∵GM⊥BC,
∴∠CGM+∠ACB=90°.
∴∠CGM=∠B.
∵△CGM 与△ABE 相似,
∴∠BAE=∠CMG 或∠BAE=∠MCG.
如图2,过点B作BF⊥x轴于F,
∵B(1,2),
∴BF=2,F(1,0),
∵A(-1,0),
∴AF=2=BF,
∴∠BAE=∠CAM,
①如图1,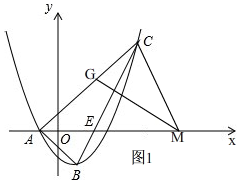 当∠BAE=∠CMG 时,
当∠BAE=∠CMG 时,
∵∠BAE=45°,
∴∠CMG=45°.
∵GM⊥BC,
∴∠MCE=45°.
∴∠MCE=∠EAB.
∵∠AEB=∠CEM,
∴△ABE∽△CME.
∴$\frac{BE}{ME}=\frac{AE}{CE}$,
∵A(-1,0),E(2,0),B(1,2),C(5,6),
∴AE=3,CE=3$\sqrt{5}$,BE=$\sqrt{5}$,
∴$\frac{\sqrt{5}}{ME}=\frac{3}{3\sqrt{5}}$,
∴ME=5,
∴M(7,0);
②如图2,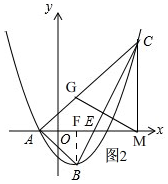 当∠BAE=∠MCG 时,
当∠BAE=∠MCG 时,
∵∠BAE=∠CAM,
∴∠MCG=∠CAM.
∴MC=MA.
设 M(x,0),
∵C(5,6),A(-1,0),
∴MC=$\sqrt{(x-5)^{2}+36}$,MA=x+1,
∴$\sqrt{(x-5)^{2}+36}$=x+1,
∴x=5,
∴M(5,0).
即:满足条件的点M的坐标为(7,0)、(5,0).
点评 此题是二次函数综合题,主要考查了待定系数法,勾股定理逆定理,锐角三角函数,相似三角形的性质,解(1)的关键是确定出抛物线解析式,解(2)的关键是判断出△ABC是直角三角形,解(3)的关键是判断出
∠CGM=∠B和∠BAE=∠CAM,是一道中等难度的中考常考题.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:解答题
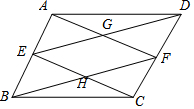 在平行四边形ABCD中,E、F分别是AB、CD的中点,AF与DE相交于点G,GE与BF相交于点H.
在平行四边形ABCD中,E、F分别是AB、CD的中点,AF与DE相交于点G,GE与BF相交于点H.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 212张 | B. | 28张 | C. | 27张 | D. | 26张 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
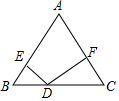 如图,在等腰三角形△ABC中,AB=AC=5,BC=6,D为底边BC上一动点(不与B、C重合)DE⊥AB,DF⊥AC,垂足分别为E、F,则DE+DF=$\frac{24}{5}$.
如图,在等腰三角形△ABC中,AB=AC=5,BC=6,D为底边BC上一动点(不与B、C重合)DE⊥AB,DF⊥AC,垂足分别为E、F,则DE+DF=$\frac{24}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2m-n=1 | B. | 2m-n=3 | C. | 2m+n=3 | D. | 2m=3n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com