
 的顶点放在D点并绕D点旋转,角的两边分别交AB边和BC边于点E和F,连接EF。求证:EF=AE+CF
的顶点放在D点并绕D点旋转,角的两边分别交AB边和BC边于点E和F,连接EF。求证:EF=AE+CF (1) 小明是这样思考的:延长BC到G,使得CG=AE,连接DG,先证△DAE≌△DCG,再证△DEF≌△DGF,请你借助图2,按照小明的思路,写出完整的证明思路。
(1) 小明是这样思考的:延长BC到G,使得CG=AE,连接DG,先证△DAE≌△DCG,再证△DEF≌△DGF,请你借助图2,按照小明的思路,写出完整的证明思路。 绕D点继续旋转,使得角
绕D点继续旋转,使得角 的两边分别和AB边延长线、BC边的延长线交于E和F,如图3所示,猜想EF、AE、CF三线段之间的数量关系并给予证明。请你帮忙解决。
的两边分别和AB边延长线、BC边的延长线交于E和F,如图3所示,猜想EF、AE、CF三线段之间的数量关系并给予证明。请你帮忙解决。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:不详 题型:单选题

| A.是中心对称图形,不是轴对称图形 |
| B.是轴对称图形,不是中心对称图形 |
| C.既是中心对称图形,又是轴对称图形 |
| D.以上都不正确 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
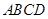 绕点
绕点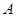 逆时针旋转
逆时针旋转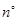 后得到正方形
后得到正方形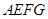 ,边
,边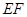 与
与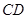 交于点
交于点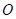 .
.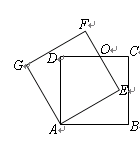
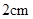 ,重叠部分(四边形
,重叠部分(四边形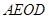 )的面积为
)的面积为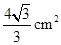 ,求旋转的角度
,求旋转的角度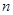 .
.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.30°. | B.40°. | C.50°. | D.80°. |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com