
【题目】今年以来,国务院连续发布了《关于加快构建大众创业万众创新支撑平台的指导意见》等一系列支持性政策,各地政府高度重视、积极响应,中国掀起了大众创业万众创新的新浪潮.某创新公司生产营销A、B两种新产品,根据市场调研,发现如下信息:
信息1:销售A种产品所获利润y(万元)与所售产品x(吨)之间存在二次函数关系y=ax2+bx,当x=1时,y=7;当x=2时,y=12.
信息2:销售B种产品所获利润y(万元)与所售产品x(吨)之间存在正比例函数关系y=2x.
根据以上信息,解答下列问题:
(1)求a,b的值;
(2)该公司准备生产营销A、B两种产品共10吨,请设计一个生产方案,使销售A、B两种产品获得的利润之和最大,最大利润是多少?
【答案】解:(1)将x=1,y=7;x=2,y=12代入y=ax2+bx得:![]() ,
,
解得:![]() .
.
答:a=﹣1,b=8;
(2)设购进A产品m吨,购进B产品(10﹣m)吨,销售A、B两种产品获得的利润之和为W元,
则W=﹣m2+8m+2(10﹣m)=﹣m2+6m+20=﹣(m﹣3)2+29,
∵﹣1<0,
∴当m=2时,W有最大值29万,
∴购进A产品3吨,购进B产品7吨,销售A、B两种产品获得的利润之和最大,最大利润是29万元.
【解析】(1)把两组数据代入二次函数解析式,然后利用待定系数法求解即可;
(2)设购进A产品m吨,购进B产品(10﹣m)吨,销售A、B两种产品获得的利润之和为W元,根据总利润等于两种产品的利润的和列式整理得到W与m的函数关系式,再根据二次函数的最值问题解答.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,E是CD上的一点,△ABF是△ADE的旋转图形.
(1)写成由△ADE顺时针旋转到△ABF的旋转中心、旋转角的度数.
(2)连接EF,判断并说明△AEF的形状.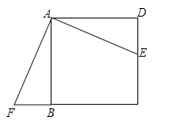
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若S△BDE:S△CDE=1:4,则S△BDE:S△ACD=( )
A.1:16
B.1:18
C.1:20
D.1:24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某绿色无公害蔬菜基地有甲、乙两种植户,他们们种植了A、B两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
种植户 | 种植A类蔬菜面积(单位:亩) | 种植B类蔬菜面积(单位:亩) | 总收入(单位:元) |
甲 | 1 | 3 | 13500 |
乙 | 2 | 2 | 13000 |
说明:不同种植户种植的同类蔬菜每亩平均收入相等
(1)求A、B两类蔬菜每亩平均收入各是多少元?
(2)今年甲、乙两种植户联合种植,计划合租50亩地用来种植A、B两类蔬菜,为了使总收入不低于16400元,问联合种植最多可以种植A类蔬菜多少亩?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有A,B,C,D四个点,且2AB=BC=3CD,若A,D两点表示的数分别为-5,6,点E为BD的中点,则该数轴上点E表示的数是____.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c过原点O、点A (2,﹣4)、点B (3,﹣3),与x轴交于点C,直线AB交x轴于点D,交y轴于点E.
(1)求抛物线的函数表达式和顶点坐标;
(2)直线AF⊥x轴,垂足为点F,AF上取一点G,使△GBA∽△AOD,求此时点G的坐标;
(3)过直线AF左侧的抛物线上点M作直线AB的垂线,垂足为点N,若∠BMN=∠OAF,求直线BM的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“1”和“4”(单位:cm),则该圆的半径为( )
A.5cm
B.![]() cm
cm
C.![]() cm
cm
D.![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有2个红球(记为红球1、红球2),1个白球、1个黑球,这些球除颜色外都相同,将球搅匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是多少;
(2)先从中任意摸出一个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表),求两次都摸到红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点0为坐标原点,抛物线y=ax2+bx+4与y轴交于点A,与x轴交于点B、C(点B在点C左侧),且OA=OC=4OB.
(1)求a,b的值;
(2)连接AB、AC,点P是抛物线上第一象限内一动点,且点P位于对称轴右侧,
过点P作PD⊥AC于点E,分别交x、y轴于点D、H,过点P作PG∥AB交AC于点F,交x轴于点G,设P(x,y),线段DG的长为d,求d与x之间的函数关系(不要求写出自变量x的取值范围);
(3)在(2)的条件下,当![]() 时,连接AP并延长至点M,连接HM交AC于点S,点R是抛物线上一动点,当△ARS为等腰直角三角形时.求点R的坐标和线段AM的长.
时,连接AP并延长至点M,连接HM交AC于点S,点R是抛物线上一动点,当△ARS为等腰直角三角形时.求点R的坐标和线段AM的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com