
【题目】近年来,我国多个城市遭遇雾霾天气,空气中可吸入颗粒(又称PM2.5)浓度升高,为应对空气污染,小强家购买了空气净化器,该装置可随时显示室内PM2.5的浓度,并在PM2.5浓度超过正常值25(mg/m3)时吸收PM2.5以净化空气.随着空气变化的图象(如图),请根据图象,解答下列问题:
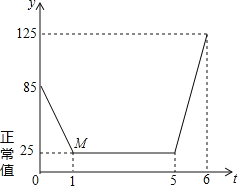
(1)写出题中的变量;
(2)写出点M的实际意义;
(3)求第1小时内,y与t的一次函数表达式;
(4)已知第5﹣6小时是小强妈妈做晚餐的时间,厨房内油烟导致PM2.5浓度升高.若该净化器吸收PM2.5的速度始终不变,则第6小时之后,预计经过多长时间室内PM2.5浓度可恢复正常?
【答案】(1)时间t和PM2.5的浓度;(2)1小时后PM2.5的浓度达到正常值25;(3)y=﹣60t+85;(4)![]()
【解析】
试题分析:(1)由函数图象可以得出变量是时间t和PM2.5的浓度;
(2)1小时后PM2.5的浓度达到正常值25;
(3)设第1小时内,y与t的一次函数表达式为y=kt+b,由待定系数法求出其解即可;
(4)设经过a小时后室内PM2.5浓度可恢复正常,由工程问题的数量关系建立方程求出其解即可.
解:(1)由函数图象,得
题中的变量是时间t和PM2.5的浓度;
(2)点M的实际意义是:
1小时后PM2.5的浓度达到正常值25;
(3)设第1小时内,y与t的一次函数表达式为y=kt+b,由题意,得
![]() ,
,
解得:![]() ,
,
∴y=﹣60t+85;
(4)设经过a小时后室内PM2.5浓度可恢复正常,由题意,得
125﹣60a=25,
解得:a=![]() .
.
答:预计经过![]() 时间室内PM2.5浓度可恢复正常.
时间室内PM2.5浓度可恢复正常.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
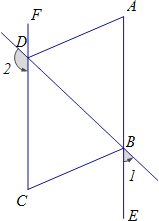
(1)AE与FC会平行吗?说明理由.
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB与x轴交于点A(﹣2,0),与x轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线y=![]() (k≠0)上,则k的值为( )
(k≠0)上,则k的值为( )

A.4 B.﹣2 C.![]() D.﹣
D.﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
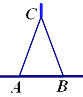
【题目】小知识:如图,我们称两臂长度相等(即![]() )的圆规为等臂圆规. 当等臂圆规的两脚摆放在一条直线上时,若张角
)的圆规为等臂圆规. 当等臂圆规的两脚摆放在一条直线上时,若张角![]() ,则底角
,则底角![]() .
.
请运用上述知识解决问题:
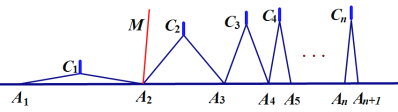
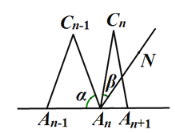
如图,![]() 个相同规格的等臂圆规的两脚依次摆放在同一条直线上,其张角度数变化如下:
个相同规格的等臂圆规的两脚依次摆放在同一条直线上,其张角度数变化如下:
![]() ,
,![]() ,
, ![]() ,
,![]() ,…
,…
(1)、①由题意可得![]() = ;
= ;
②若![]() 平分
平分![]() ,则
,则![]() = ;
= ;
(2)、![]() = (用含
= (用含![]() 的代数式表示);
的代数式表示);
(3)、当![]() 时,设
时,设![]() 的度数为
的度数为![]() ,
,![]() 的角平分线
的角平分线![]() 与
与![]() 构成的角的度数为
构成的角的度数为![]() ,那么
,那么![]() 与
与![]() 之间的等量关系是 ,请说明理由. (提示:可以借助下面的局部示意图)
之间的等量关系是 ,请说明理由. (提示:可以借助下面的局部示意图)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是( ).
A.锐角三角形的三条高线、三条中线、三条角平分线分别交于一点
B.钝角三角形有两条高线在三角形外部
C.直角三角形只有一条高线
D.任意三角形都有三条高线、三条中线、三条角平分线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:
①abc>0;②2a+b=0;③当x≠1时,a+b>ax2+bx;④a﹣b+c>0.
其中正确的有 .
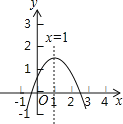
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=k1x+b与反比例函数y=![]() 相交于A(﹣1,2),B(2,m)两点,与y轴相交于点C.
相交于A(﹣1,2),B(2,m)两点,与y轴相交于点C.
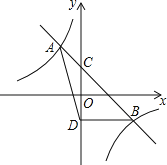
(1)求k1、k2、m的值;
(2)若点D与点C关于x轴对称,求△ABD的面积;
(3)若M(x1,y1)、N(x2,y2)是反比例函数y=![]() 图象上的两点,且x1<x2时,y1>y2,指出点M、N各位于坐标系的哪个象限,并简要说明理由.
图象上的两点,且x1<x2时,y1>y2,指出点M、N各位于坐标系的哪个象限,并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了丰富学生的校园生活,准备购进一批篮球和足球.其中篮球的单价比足球的单价多40元,用1500元购进的篮球个数与900元购进的足球个数相等.
(1)篮球和足球的单价各是多少元?
(2)该校打算用1000元购买篮球和足球,问恰好用完1000元,并且篮球、足球都买有的购买方案有哪几种?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点P(x,y)在第三象限,且点P到x轴的距离为3,到y轴的距离为2,则点P的坐标是( )
A. (-2,-3) B. (-2,3) C. (2,-3) D. (2,3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com