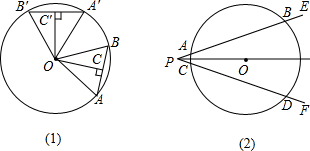
(1)证明:如图1,过O作OM⊥AB于M,ON⊥CD于N,
则∠OMB=∠OND=90°,
∵PO平分∠EPF,
∴OM=ON,
在Rt△OMB和Rt△OND中

∴Rt△OMB≌Rt△OND(HL),
∴BM=DN,
∵OM⊥AB,ON⊥CD,OM、ON过O,
∴AB=2BM,CD=2DN,
∴AB=CD;
(2)还成立,
证明:如图2,当P在⊙O上时,

∵由(1)知:BM=DN,AB=2BM,CD=2DN,
∴AB=CD;
当P在⊙O内时,如图3,

∵由(1)知:BM=DN,AB=2BM,CD=2DN,
∴AB=CD.
分析:(1)过O作OM⊥AB于M,ON⊥CD于N,求出ON=OM,证△OMB≌△OND,推出BM=DN,根据垂径定理得出AB=2BM,CD=2DN,即可得出答案;
(2)过O作OM⊥AB于M,ON⊥CD于N,求出ON=OM,证△OMB≌△OND,推出BM=DN,根据垂径定理得出AB=2BM,CD=2DN,即可得出答案.
点评:本题考查了垂径定理,角平分线性质,全等三角形的性质和判定的应用,主要考查学生运用定理进行推理的能力,题目比较好,证明过程类似.








 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案