
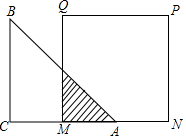
 如图,已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时点A与点M重合,让△ABC向右移动,最后让点A与点N重合.
如图,已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时点A与点M重合,让△ABC向右移动,最后让点A与点N重合.分析 (1)根据图形及题意所述可得出重叠部分是等腰直角三角形,从而根据MA的长度可得出y与x的关系;
(2)根据开始时点A与点M重合,让△ABC向右移动,最后让点A与点N重合,可得0≤AM≤10,据此得出自变量的取值范围;
(3)根据自变量的取值,运用(1)中的函数解析式,通过计算求得重叠部分的面积即可.
解答  解:(1)由题意知,△ABC是等腰直角三角形,∠AMQ=90°,
解:(1)由题意知,△ABC是等腰直角三角形,∠AMQ=90°,
∴重叠部分是等腰直角三角形,
又∵线段AM=x,
∴y=$\frac{1}{2}$x2;
(2)∵开始时点A与点M重合,让△ABC向右移动,最后让点A与点N重合,
∴0≤AM≤10,即0≤x≤10,
故自变量x的取值范围是:0≤x≤10;
(3)当x=MA=4cm时,重叠部分的面积y=$\frac{1}{2}$×42=8(cm2).
点评 本题属于四边形综合题,主要考查了等腰直角三角形的性质,正方形的性质以及二次函数求值的综合应用,判断出重叠部分是等腰直角三角形是解决问题的关键.等腰直角三角形是一种特殊的三角形,具有所有三角形的性质,还具备等腰三角形和直角三角形的所有性质.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案科目:初中数学 来源: 题型:解答题
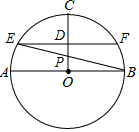 如图,⊙O中,半径CO垂直于直径AB,D为OC的中点,过D作弦EF∥AB,EB与OC交于点P.
如图,⊙O中,半径CO垂直于直径AB,D为OC的中点,过D作弦EF∥AB,EB与OC交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 34和43 | B. | -($\frac{1}{2}$)3和(-$\frac{1}{2}$)3 | C. | -22和 (-2 )2 | D. | |-3|和-|-3| |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com