练习册

  • 练习册
  • 试题
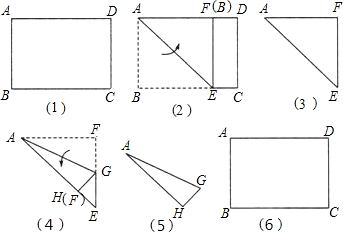
    精英家教网 > 初中数学 > 题目详情
    如图L形纸片的面积用代数式表示为（　　）
    分析：首先把图形分割成规则图形，L形纸片的面积，=S1+S2，再分别表示出S1、S2的面积即可选出答案．
    解答：解：如图所示：
    L形纸片的面积，
    =S1+S2，
    =d（a-c）+bc，
    =ad-cd+bc，
    =ad+c（b-d），
    故选：C．
    点评：此题主要考查了列代数式，关键是根据图形，把不规则的图形划分为规则图形．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

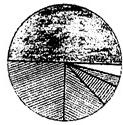    精英家教网王老师为调动学生参加班级活动的积极性，给每位学生设计了一个如图所示的面积为1的圆形纸片，若在活动中表现优胜者，可依次用色彩纸片覆盖圆面积的
    1
    2
    ，
    1
    4
    ，
    1
    8
    …．请你根据数形结合的思想，依据图形的变化，推断当n为整数时，
    1
    2
    +
    1
    4
    +
    1
    8
    +…+
    1
    2n
    =
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图（1），矩形纸片ABCD中，AD=28cm，AB=20cm．
    （1）将矩形ABCD沿折线AE对折，使AB与AD边重合，B点落在F点处（如图（2）所示）；再剪去四边形CEFD，余下的部分如图（3）所示．若将余下的纸片展形，则所得的四边形ABEF的形状是
     
    ，它的面积为
     
    cm2．
    （2）将图（3）中的纸片沿折线AG对折，使AF与AE边重合，F点落在H点处（如图（4）所示），再沿HG将△HE剪去，余下的部分如图（5）所示．把图（5）的纸片完全展开，请你在图（6）的矩形ABCD中画出展开后图形的示意图，剪去的部分用阴影表示，折痕用虚线表示．
    （3）求图（5）中的纸片完全展形后图形的面积（结果保留整数）．精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

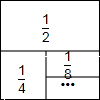    我国著名数学家华罗庚曾说过：“数形结合百般好，隔裂分家万事非．”如图，在一个边长为1的正方形纸版上，依次贴上面积为
    1
    2
    ，
    1
    4
    ，
    1
    8
    …
    1
    2n
    ，的矩形彩色纸片（n为大于1的整数）．
    请你用“数形结合”的思想，依数形变化的规律，计算
    1
    2
    +
    1
    4
    +
    1
    8
    +…+
    1
    2n
    =
    1-
    1
    2n
    1-
    1
    2n
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：单选题

    如图L形纸片的面积用代数式表示为


    1. A.
      ad+bc
    2. B.
      c（b-d）+d（a-c）
    3. C.
      ad+c（b-d）
    4. D.
      ab-cd

    查看答案和解析>>

    同步练习册答案