

分析 (1)观察图形可确定:方法一,大正方形的面积为(m+n)2,四个小长方形的面积为4mn,中间阴影部分的面积为S=(m+n)2-4mn;
方法二,图2中阴影部分为正方形,其边长为m-n,所以其面积为(m-n)2.
(2)观察图形可确定,大正方形的面积减去四个小长方形的面积等于中间阴影部分的面积,即(m+n)2-4mn=(m-n)2.
(3)根据(2)的关系式代入计算即可求解.
解答 解:(1)方法一:S小正方形=(m+n)2-4mn.
方法二:S小正方形=(m-n)2.
(2)(m+n)2,(m-n)2,mn这三个代数式之间的等量关系为(m+n)2-4mn=(m-n)2.
(3)∵x+y=9,xy=14,
∴x-y=±$\sqrt{(x+y)^{2}-4xy}$=±5.
故答案为:(m+n)2-4mn,(m-n)2;(m+n)2-4mn=(m-n)2.
点评 本题是完全平方式的实际应用,完全平方式经常与正方形的面积公式和长方形的面积公式联系在一起,要学会观察图形.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:填空题
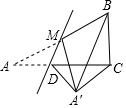 如图所示,Rt△ABC中,∠A=30°,BC=6,M是AB中点,D是线段AC上任意一点(D不与A、C重合),沿直线MD把∠A翻折,使点A落在A′处,当△A′BC为等腰三角形时,AD的长是2$\sqrt{3}$或6.
如图所示,Rt△ABC中,∠A=30°,BC=6,M是AB中点,D是线段AC上任意一点(D不与A、C重合),沿直线MD把∠A翻折,使点A落在A′处,当△A′BC为等腰三角形时,AD的长是2$\sqrt{3}$或6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知某学校A与直线公路BD相距3000米,且与该公路上一个车站D相距5000米,现要在公路边建一个超市C,使之与学校A及车站D的距离相等,那么该超市与车站D的距离是多少米?
如图,已知某学校A与直线公路BD相距3000米,且与该公路上一个车站D相距5000米,现要在公路边建一个超市C,使之与学校A及车站D的距离相等,那么该超市与车站D的距离是多少米?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,∠1=∠2,下列选项中不能证明△ABC∽△ADE的是( )
如图,∠1=∠2,下列选项中不能证明△ABC∽△ADE的是( )| A. | ∠B=∠D | B. | ∠C=∠E | C. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | D. | $\frac{AD}{AB}$=$\frac{DE}{BC}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 这2000名考生是总体的一个样本 | B. | 每位考生的数学成绩是个体 | ||
| C. | 10万名考生是个体 | D. | 10万名考生是总体 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$+3$\sqrt{3}$=6$\sqrt{3}$ | B. | 5$\sqrt{5}$-2$\sqrt{3}$=3$\sqrt{2}$ | C. | $\sqrt{3}$÷$\sqrt{2}$=$\frac{\sqrt{6}}{2}$ | D. | ($\sqrt{5}$)-2=$\frac{2}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
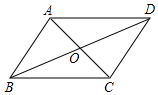 如图,平行四边形ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )
如图,平行四边形ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )| A. | 26 | B. | 20 | C. | 17 | D. | 13 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com