
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��������AOB�Ķ���A��B�ֱ������������ϣ�OΪԭ�㣬��A������Ϊ��6��0������B������Ϊ��0��8��������M�ӵ�O��������OA���յ�A��ÿ��1����λ���ٶ��˶���ͬʱ����N�ӵ�A��������AB���յ�B��ÿ�� ![]() ����λ���ٶ��˶�����һ�����㵽���յ�ʱ����һ������Ҳ��ֹ֮ͣ�˶����趯��M��N�˶���ʱ��Ϊt�루t��0����
����λ���ٶ��˶�����һ�����㵽���յ�ʱ����һ������Ҳ��ֹ֮ͣ�˶����趯��M��N�˶���ʱ��Ϊt�루t��0����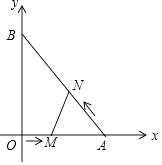
��1����t=3��ʱ��ֱ��д����N�����ꣻ
��2���ڴ��˶��Ĺ����У���MNA������Ƿ�������ֵ�������ڣ���������ֵ���������ڣ���˵�����ɣ�
��3����tΪ��ֵʱ����MNA��һ�����������Σ�
���𰸡�
��1��
�⣺��NC��OA��C��
��t=3ʱ��AN=3�� ![]() =5��
=5��
��CN=ANsin��OAB=5�� ![]() =4��AC=ANcos��OAB=5��
=4��AC=ANcos��OAB=5�� ![]() =3��
=3��
��OC=OA��AC=3��
��N��3��4��
�ʴ�ΪN��3��4����
��2��
�⣺�����⣬AN= ![]() t��AM=OA��OM=6��t��
t��AM=OA��OM=6��t��
NC=NAsin��BAO= ![]() t
t ![]() =
= ![]() t��
t��
��S��MNA= ![]() AMNC=
AMNC= ![]() ����6��t����
����6��t���� ![]() t��
t��
=�� ![]() ��t��3��2+6��
��t��3��2+6��
���MNA����������ֵ�������ֵΪ6��
��3��
�⣺���ⷨ1��AM=6��t��AN= ![]() t ��0��t��6����
t ��0��t��6����
��AC=ANcos��BAO=t��
�ٵ�AM=ANʱ��6��t= ![]() t���� t=
t���� t= ![]() ��
��
�ڵ�MN=ANʱ����NC��ֱƽ���߶�MA��
��MC=AC=t
��OM+MC+CA=OA
��t+t+t=6 ���t=2
�۵�MN=MAʱ����DΪ�߶�AN���е㣬�� MD��ֱƽ���߶�AN
��AD= ![]() AN=
AN= ![]() ��
��
�֡�cos��DAM=cos��OAB ����ߡ�DAM�ס�OAB��
�� ![]() ��
�� ![]() ��� t=
��� t= ![]() ��
��
���ϣ���t��ֵȡ 2�� ![]() ��
�� ![]() ʱ����MAN�ǵ��������Σ�
ʱ����MAN�ǵ��������Σ�
���ⷨ2��AN= ![]() t��NC=
t��NC= ![]() t��AC=ANcos��BAO=t��
t��AC=ANcos��BAO=t��
��OC=OA��AC=6��t��
��MC=|OC��OM|=|6��t��t|=|6��2t|
Rt��NCM�� NM2=MC2+NC2
��NM= ![]() =
= ![]() ��
��
�� ![]() ��
��
�֣�AM=6��t��AN= ![]() t��0��t��6����
t��0��t��6����
�ٵ�MN=ANʱ��MN2=AN2
�� ![]() =
= ![]() ��
��
����t2��8t+12=0��t1=2��t2=6����ȥ����
�ڵ�MN=MAʱ��MN2=MA2
�� ![]() =��6��t��2��
=��6��t��2��
���� ![]() t2��12t=0��t1=0����ȥ����t2=
t2��12t=0��t1=0����ȥ����t2= ![]() ��
��
�۵�AM=ANʱ��6��t= ![]() t����t=
t����t= ![]() ��
��
���ϣ���t��ֵȡ 2�� ![]() ��
�� ![]() ʱ����MAN�ǵ��������Σ�
ʱ����MAN�ǵ��������Σ�
����������1����NC��OA��C����Rt��ANC�У����NC��AC���ɽ�����⣻��2������N��NC��OA��C�������⣬AN= ![]() t��AM=OA��OM=6��t��NC=NAsin��BAO=
t��AM=OA��OM=6��t��NC=NAsin��BAO= ![]() t
t ![]() =
= ![]() t����S��MNA=
t����S��MNA= ![]() AMNC=
AMNC= ![]() ����6��t����
����6��t���� ![]() t=��
t=�� ![]() ��t��3��2+6�����ݶ��κ��������ʼ��ɽ�����⣻��3�����������η����г����̼��ɽ�����⣮��
��t��3��2+6�����ݶ��κ��������ʼ��ɽ�����⣻��3�����������η����г����̼��ɽ�����⣮��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ͼ4�У�����ABCD�ı߳�Ϊ3����A=60�㣬��M��AD����һ�㣬��DM= ![]() AD����N������AB��BC�ϵ�һ�����㣮
AD����N������AB��BC�ϵ�һ�����㣮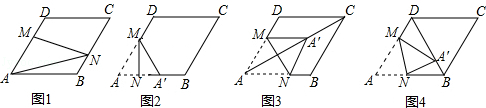
��1����ͼ1����N��BC���ϣ���MN���Խ���AC��BD�Ľ���ʱ�����߶�AN�ij���Ϊ ��
��2������N��AB����ʱ������AMN��MN���۵õ�
��A��MN����ͼ2��
������A������AB���ϣ����߶�AN�ij���Ϊ ![]() ��
��
�ڵ���A�����ڶԽ���AC��ʱ����ͼ3����֤���ı���AM A��N�����Σ�
�۵���A�����ڶԽ���BD��ʱ����ͼ4���� ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������������ׯC��D����ͬһˮƽ���ϣ�һ�������ڿ�����6ǧ��/Сʱ���ٶ���MN����ˮƽ���У�����MN��C��D��ͬһǦֱƽ���ڣ����÷�������������ׯC�����Ϸ�A��ʱ����á�NAD=60�㣻�÷�������A������40������B��ʱ����á�ABD=75�㣮���ׯC��D��ľ��루 ![]() ȡ1.73�������ȷ��0.1ǧ�ף�
ȡ1.73�������ȷ��0.1ǧ�ף� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�ٽ����о��õĿ��ٷ�չ���ӿ��·���裬ij���ٹ�·���蹤������������AB����ͼ����ɽ��һ��C���BC����Ϊ200m����CAB=54�㣬��CBA=30�㣬������AB�ij������ο����ݣ�sin54���0.81��cos54���0.59��tan54���1.38�� ![]() ��1.73����ȷ����λ��
��1.73����ȷ����λ�� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC������ֱ�ߺ�Բ�棬��������Ҫ����ͼ��������ͼ�ۼ�����Ҫ��д��������������Ҫ����գ� 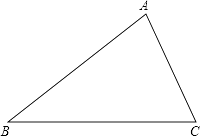
��1������ABC��ƽ����BD��AC�ڵ�D��
��2�����߶�BD�Ĵ�ֱƽ���߽�AB�ڵ�E����BC�ڵ�F���ɣ�1������2���ɵã��߶�EF���߶�BD�Ĺ�ϵΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУΪ�˸��ư�ѧ�������ƻ�����һ��ʵ��ͶӰ�Ǻ�һ��̨ʽ���ԣ���Ͷ�꣬����1̨ʵ��ͶӰ�Ǻ�2̨���Թ�����11000Ԫ������2̨ʵ��ͶӰ�Ǻ�3̨���Թ�����18000Ԫ��
��1������1̨ʵ��ͶӰ�Ǻ�1̨���Ը������Ԫ��
��2�����ݸ�Уʵ��������蹺��ʵ��ͶӰ�Ǻ�̨ʽ���Ե�����Ϊ50̨��Ҫ������ܷ��ò�����180000Ԫ����У����ܹ������̨���ԣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����xΪ�Ա����Ķ��κ���y=x2��2��b��2��x+b2��1��ͼ�����������ޣ���ʵ��b��ȡֵ��Χ�ǣ� ��
A.b�� ![]()
B.b��1��b�ܩ�1
C.b��2
D.1��b��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��D�ڡ�ABC��BC���ϣ�DE��AC��AB��E��DF��AB��AC��F�� 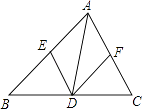
��1����֤��AE=DF��
��2����ADƽ�֡�BAC�����ж��ı���AEDF����״����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����߳�Ϊ3�������εĶԽ��߳�Ϊa�����й���a������˵���� ��a����������
��a�����������ϵ�һ��������ʾ��
��3��a��4��
��a��18������ƽ������
���У�������ȷ˵��������ǣ� ��
A.�٢�
B.�ڢ�
C.�٢ڢ�
D.�٢ۢ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com