
ЁОЬтФПЁПвбжЊЃКШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌAЃЈ2ЃЌЃ1ЃЉЃЌвдMЃЈЃ1ЃЌ0ЃЉЮЊдВаФЃЌвдAMЮЊАыОЖЕФдВНЛyжсгкЕуBЃЌСЌНсBMВЂбгГЄНЛЁбMгкЕуCЃЌЖЏЕуPдкЯпЖЮBCЩЯдЫЖЏЃЌГЄЮЊ![]() ЕФЯпЖЮPQЁЮxжсЃЈЕуQдкЕуPгвВрЃЉЃЌСЌНсAQЃЎ
ЕФЯпЖЮPQЁЮxжсЃЈЕуQдкЕуPгвВрЃЉЃЌСЌНсAQЃЎ
ЃЈ1ЃЉЧѓЁбMЕФАыОЖГЄКЭЕуBЕФзјБъЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌСЌНсACЃЌНЛЯпЖЮPQгкЕуNЃЌ
ЂйЧѓACЫљдкжБЯпЕФНтЮіЪНЃЛ
ЂкЕБPN=QNЪБЃЌЧѓЕуQЕФзјБъЃЛ
ЃЈ3ЃЉЕуPдкЯпЖЮBCЩЯдЫЖЏЕФЙ§ГЬжаЃЌЧыжБНгаДГіAQЕФзюаЁжЕКЭзюДѓжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉАыОЖЮЊ![]() ЃЌЕуBЃЈ0ЃЌ3ЃЉЃЛ
ЃЌЕуBЃЈ0ЃЌ3ЃЉЃЛ
ЃЈ2ЃЉЂйyACЃН![]() xЃ2ЃЌЂкЕуQзјБъЮЊЃЈЃ
xЃ2ЃЌЂкЕуQзјБъЮЊЃЈЃ![]() ЃЌЃ
ЃЌЃ ![]() ЃЉ
ЃЉ
ЃЈ3ЃЉAQзюаЁжЕЮЊ![]() ЃЌAQзюДѓжЕЮЊ
ЃЌAQзюДѓжЕЮЊ![]()
ЁОНтЮіЁПЪдЬтЗжЮіЃК(1)ЁЂЙ§ЕуAзїAEЁЭxжсЃЌдђAEЃН1ЃЌMEЃН3ЃЌДгЖјЕУГідВЕФАыОЖЃЌШЛКѓИљОнRtЁїMOBЕФЙДЙЩЖЈРэЕУГіOBЕФГЄЖШЃЌЕУГіЕуBЕФзјБъЃЛ(2)ЁЂЪзЯШЩшжБЯпACЕФНтЮіЪНЮЊЃКy=kx+bЃЌИљОнжааФЖдГЦЕФаджЪЕУГіЕуCЕФзјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіКЏЪ§НтЮіЪНЃЛИљОнЬтвтЕУГіжБЯпBCЕФНтЮіЪНЮЊy=3x+3ЃЌЩшЕуPЕФзјБъЮЊ(xЃЌ3x+3)ЃЌДгЖјЕУГіЕуNЕФзјБъЃЌШЛКѓИљОнЕуNдкжБЯпACЩЯЧѓГіxЕФжЕЃЌДгЖјЕУГіЕуQЕФзјБъЃЛ(3)ЁЂИљОнзюаЁжЕКЭзюДѓжЕЕФМЦЫуЗЈдђвдМАЙДЙЩЖЈРэЕУГізюжЕ.
ЪдЬтНтЮіЃКЃЈ1ЃЉЙ§ЕуAзїAEЁЭxжсЃЌдђAEЃН1ЃЌMEЃН3ЃЌЁрAMЃН![]() ЃЌМДАыОЖЮЊ
ЃЌМДАыОЖЮЊ![]()
ЫљвдBMЃН![]() ЃЌЁпOMЃН1ЃЌЁрOBЃН3ЃЌМДЕуBЃЈ0ЃЌ3ЃЉ
ЃЌЁпOMЃН1ЃЌЁрOBЃН3ЃЌМДЕуBЃЈ0ЃЌ3ЃЉ
ЃЈ2ЃЉЂйЩшНтЮіЪНЮЊЩшyACЃНkxЃЋb гЩЬтвтЕУЕуCгыЕуBЙигкЕуMГЩжааФЖдГЦЃЌ
ЁрЕуCЃЈЃ2ЃЌЃ3ЃЉ гжЕуAЃЈ2ЃЌЃ1ЃЉ
МДЕБxЃН2ЪБЃЌyЃНЃ1ЃЛЕБxЃНЃ2ЪБЃЌyЃНЃ3 НтЕУkЃН![]() ЃЌbЃНЃ2 ЁрyACЃН
ЃЌbЃНЃ2 ЁрyACЃН![]() xЃ2
xЃ2
ЂкПЩЧѓyBCЃН3xЃЋ3ЃЌЩшЕуPЃЈxЃЌ3xЃЋ3ЃЉ гЩЬтвтЕУЕуNЮЊ(xЃЋ![]() ЃЌ3xЃЋ3)
ЃЌ3xЃЋ3)
ЁпЕуNТфдкACЩЯЃЌЫљвд3xЃЋ3ЃН![]() ( xЃЋ
( xЃЋ![]() )Ѓ2 НтЕУxЃНЃ
)Ѓ2 НтЕУxЃНЃ![]()
ЫљвдЕуQзјБъЮЊЃЈЃ![]() ЃЌЃ
ЃЌЃ![]() ЃЉ
ЃЉ
ЃЈ3ЃЉAQзюаЁжЕЮЊ![]() ЃЌ AQзюДѓжЕЮЊ
ЃЌ AQзюДѓжЕЮЊ![]()


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМЦЫуЃК
ЃЈ1ЃЉМЦЫуЃКЃЈЉ2016ЃЉ0+ЃЈ ![]() ЃЉЉ2+ЃЈЉ3ЃЉ3ЃЛ
ЃЉЉ2+ЃЈЉ3ЃЉ3ЃЛ
ЃЈ2ЃЉМђЫуЃК982 -97ЁС99ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊЯпЖЮABЕФСНИіЖЫЕуЗжБ№ЪЧAЃЈ1ЃЌ2ЃЉЃЌBЃЈ2ЃЌ0ЃЉЃЌНЋЯпЖЮABЦНвЦКѓЕУЕНЯпЖЮCDЃЌШєЕуAЕФЖдгІЕуЪЧЕуCЃЈ3ЃЌaЃЉЃЌЕуBЕФЖдгІЕуЪЧЕуDЃЈbЃЌ1ЃЉЃЌдђaЉbЕФжЕЪЧЃЈ ЃЉ
A.Љ1
B.0
C.1
D.2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
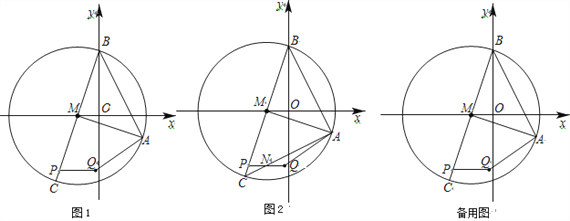
ЁОЬтФПЁПШчЭМЃЌЕШБпШ§НЧаЮABCЕФБпГЄЮЊ6ЃЌдкACЃЌBCБпЩЯИїШЁвЛЕуEЃЌFЃЌСЌНгAFЃЌBEЯрНЛгкЕуPЃЌЧвAE=CF.
(1)ЧѓжЄЃКAF=BEЃЌВЂЧѓЁЯFPBЕФЖШЪ§ЃЛ
(2)ШєAE=2ЃЌЪдЧѓAPЁЄAFЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
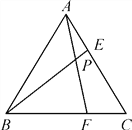
ЁОЬтФПЁПШчЭМЃЌЪЧгЩСНИіе§ЗНаЮзщГЩЕФГЄЗНаЮЛЈЬГABCDЃЌаЁУїДгЖЅЕуAбизХЛЈЬГМфаЁТЗжБЕНзпЕНГЄБпжаЕуOЃЌдйДгжаЕуOзпЕНе§ЗНаЮOCDFЕФжааФO1 ЃЌ дйДгжааФO1зпЕНе§ЗНаЮO1GFHЕФжааФO2 ЃЌ гжДгжааФO2зпЕНе§ЗНаЮO2IHJЕФжааФO3 ЃЌ дйДгжааФO3зп2зпЕНе§ЗНаЮO3KJPЕФжааФO4 ЃЌ вЛЙВзпСЫ31 ![]() mЃЌдђГЄЗНаЮЛЈЬГABCDЕФжмГЄЪЧ ЃЎ
mЃЌдђГЄЗНаЮЛЈЬГABCDЕФжмГЄЪЧ ЃЎ 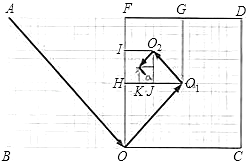
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙужне§ЮШВНЭЦНјБЬЕРНЈЩшЃЌгЊдьЁАЫЎЧхАЖТЬЁЂгуЯшЧГЕзЁЂЫЎВнЗсУРЁЂАз№иГЩШКЁБЕФЩњЬЌРШЕРЃЌЪЙжЎГЩЮЊРЯАйаеУРКУЩњЛюЕФКУШЅДІЃЌЕННёФъЕзИїЧјЭъГЩБЬЕРЪдЕуНЈЩшЕФГЄЖШЗжБ№ЮЊЃЈЕЅЮЛЃКЧЇУзЃЉЃК5ЃЌ5.2ЃЌ5ЃЌ5ЃЌ5ЃЌ6.4ЃЌ6ЃЌ5ЃЌ6.68ЃЌ48.4ЃЌ6.3ЃЌетзщЪ§ОнЕФжкЪ§ЪЧЃЈ ЃЉ
A. 5B. 5.2C. 6D. 6.4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌгУСПНЧЦїЖШСПМИИіНЧЕФЖШЪ§,ЯТСаНсТлжае§ШЗЕФЪЧЃЈ ЃЉ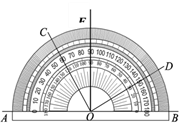
A.ЁЯBOC=60Ёу
B.ЁЯCOAЪЧЁЯEOD ЕФгрНЧ
C.ЁЯAOC=ЁЯBOD
D.ЁЯAODгыЁЯCOEЛЅВЙ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигкxЕФвЛдЊЖўДЮЗНГЬx2+mx+n=0ЕФСНИіЪЕЪ§ИљЗжБ№ЮЊx1=-2ЃЌx2=4ЃЌдђm+n=______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЁїABCжаЃЌABЃНACЃЌЧѓжЄЁЯBЃМ90ЁуЃЌЯТУцаДГіСЫгУЗДжЄЗЈжЄУїЙ§ГЬжаЕФЫФИіВНжшЃКЂйЫљвдЁЯBЃЋЁЯCЃЋЁЯAЃО180ЁуЃЌетгыШ§НЧаЮФкНЧКЭЖЈРэЯрУЌЖмЃЛЂкЫљвдЁЯBЃМ90ЁуЃЛЂлМйЩшЁЯBЁн90ЁуЃЛЂмФЧУДгЩABЃНACЃЌЕУЁЯBЃНЁЯCЁн90ЁуЃЌМДЁЯBЃЋЁЯCЁн180Ёу.етЫФИіВНжше§ШЗЕФЫГађгІЪЧ_________(ЬюађКХ)ЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com