
已知⊙O1与⊙O2的半径分别为R、r,且R≥r,R、r是方程x2-5x+2=0的两根,设O1O2=d,那么
(1)若d=![]() 时,试判定⊙O1与⊙O2的位置关系:
时,试判定⊙O1与⊙O2的位置关系:
(2)若d=3时,试判定⊙O1与⊙O2的位置关系;
(3)若d=4.5时,试判定⊙O1与⊙O2的位置关系;
(4)若两圆相切,求d的取值范围.
|
解∵R、r是x2-5x+2=0的两根,∴R+r=5,R·r=2, ∵Δ=25-8>0. ∴R,r不等,又∵R≥r,∴R>r,∴R-r>0. ∴R-r= (1)∵d= (2)∵d=3< (3)∵d=4.5,∴ ∴两圆相交. (4)要使⊙O1与⊙O2相切,则d=R-r或d=R+r, ∴d= 思路点拨:先分别求出R+r与R-r,然后比较d与R+r、R-r的大小作出判断. 评注:本题主要考查用圆的半径与圆心距的数量关系来判断圆的位置关系,需要注意的是判定两圆相交,必须d>R-r且d<R+r两个条件同时成立,而两圆相切包括内切和外切两种情况. |


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
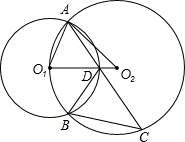 如图,已知⊙O1与⊙O2的半径分别为r1,r2,⊙O2经过⊙O1的圆心O1,且两圆相交于A,B两点,C为⊙O2上的点,连接AC交⊙O1于D点,再连接BC,BD,AO1,AO2,O1O2,有如下四个结论:①∠BDC=∠AO1O2;②
如图,已知⊙O1与⊙O2的半径分别为r1,r2,⊙O2经过⊙O1的圆心O1,且两圆相交于A,B两点,C为⊙O2上的点,连接AC交⊙O1于D点,再连接BC,BD,AO1,AO2,O1O2,有如下四个结论:①∠BDC=∠AO1O2;②| BD |
| BC |
| r1 |
| r2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com