练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知多项式A=.

    求【解析】
    （1）化简多项式A； （2）若，求A的值.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    10．解方程：
    （1）4-2（x-3）=3x
    （2）1-$\frac{3x-2}{4}=\frac{x-2}{2}$．

    查看答案和解析>>

    科目：初中数学 来源：2017届河南省周口市招第一次模拟考试数学试卷（解析版） 题型：判断题

    如图，在平面直角坐标系中，直线y＝－2x＋10与x轴，y轴相交于A，B两点，点C的坐标为（8，4），连接AC，BC．

    （1）求过O，A，C三点的抛物线的解析式，并判断△ABC的形状；

    （2）动点P从O点出发，沿OB以每秒两个单位长度的速度向点B运动，同时动点Q从点B出发，沿BC以每秒一个单位长度的速度向点C运动，规定其中一个动点到达端点时另一个动点也随之停止运动，设运动时间为t秒，当t为何值时，PA＝QA？；

    （3）在抛物线的对称轴上，是否存在点M，使A，B，M为顶点的三角形是等腰三角形？若存在，直接写出M点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2017届河南省周口市招第一次模拟考试数学试卷（解析版） 题型：单选题

    如图所示是某个几何体的三视图，该几何体是

    A. 圆锥 B. 三棱锥 C. 圆柱 D. 三棱柱

    查看答案和解析>>

    科目：初中数学 来源：2017届广东省广州市九年级下学期3月月考数学试卷（解析版） 题型：判断题

    类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做等邻边四边形.

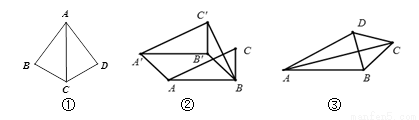
    （1）如图①，四边形ABCD中，AC平分∠BAD，∠B=∠D. 求证：四边形ABCD为等邻边四边形.

    （2）如图②，Rt△ABC中，∠ABC=90°，AB=2，BC=1，将△ABC沿∠ABC的平分线BB′的方向平移，得到△A′B′C′，连接AA′、BC′，若平移后的四边形ABC′A′是等邻边四边形，且满足BC′=AB，求平移的距离.

    （3）如图③，在等邻边四边形ABCD中，AB=AD，∠BAD+∠BCD=90°，AC和BD为四边形对角线，△BCD为等边三角形，试探究AC和AB的数量关系.

    查看答案和解析>>

    科目：初中数学 来源：2017届广东省广州市九年级下学期3月月考数学试卷（解析版） 题型：填空题

    一个几何体的三视图如图示，根据图示的数据计算该几何体的全面积为_______（结果保留）．

    查看答案和解析>>

    科目：初中数学 来源：2017届广东省广州市九年级下学期3月月考数学试卷（解析版） 题型：单选题

    在一次科技作品制作比赛中，某小组八件作品的成绩（单位：分）分别是：7，10，9，8，7，9，9，8．对这组数据，下列说法正确的是（ ）．

    A. 中位数是8 B. 众数是9 C. 平均数是8 D. 极差是7

    查看答案和解析>>

    科目：初中数学 来源：2017届江苏省徐州市九年级下学期第一次（3月）月考数学试卷（解析版） 题型：填空题

    若a2﹣3a+2=0，则1+6a﹣2a2=__．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，已知抛物线y=k（x+2）（x-4）（k为常数，且k＞0）与x轴的交点为A、B，与y轴的交点为C，经过点B的直线y=-$\frac{1}{2}$x+b与抛物线的另一个交点为D．
    （1）若点D的横坐标为x=-4，求这个一次函数与抛物线的解析式；
    （2）若直线m平行于该抛物线的对称轴，并且可以在线段AB间左右移动，它与直线BD和抛物线分别交于点E、F，求当m移动到什么位置时，EF的值最大，最大值是多少？
    （3）问原抛物线在第一象限是否存在点F，使得△APB∽△ABC？若存在，请直接写出这时k的值；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案