Question

17．如图①，正方形ABDE、CDFI、EFGH的面积分别为17、10、13，图②中的DPQR为矩形，对照图②求图①中ABCIGH的面积．

Answer 1

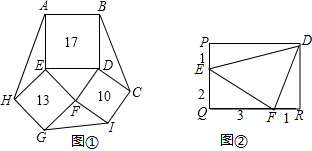
分析 首先求出△BCD，△GFI，△AEH的面积即可，然后△DEF的面积通过图乙求解．

解答 解：∵DF=DC，DE=DB，且∠EDF+∠BDC=180°，
根据三角形的面积公式得S_△AHE=S_△DEF，
同理S_△BDC=S_△GFI=S_△DEF，
S_△AHE+S_△BDC+S_△GFI=3×S_△DEF，
S_△DEF=3×4-2-3-1.5=5.5，
∴六边形ABCIGH的面积为S_△AHE+S_△BDC+S_△GFI+S_△DEF+17+13+10
=62．
答：六边形ABCIGH的面积为62．

点评 此题考查了正方形的性质以及三角形面积的计算．注意解本题的关键是找到：S_△AHE+S_△BDC+S_△GFI=3×S_△DEF．