
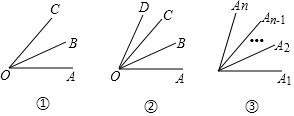
分析 (1)根据角的概念,列出图中所有角,即可得;
(2)根据角的概念,列出图中所有角,即可得;
(3)当图中有n条射线时,每条射线都与(n-1)条射线构成了(n-1)个角,则共有n(n-1)个角,由于两条射线构成一个角,因此角的总数为:$\frac{n(n-1)}{2}$.
解答 解:(1)在如图①中,角有∠AOB、∠AOC、∠BOC,共1+2=3个;
(2)在如图②中,角有∠AOB、∠AOC、∠AOD、∠BOC、∠BOD、∠COD,共1+2+3=6个;
(3)在如图③中,共有1+2+3+…+n-1=$\frac{n(n-1)}{2}$个.
点评 本题主要考查角的概念和图形的变化规律,解答此类规律型问题,一定要弄清题目的规律,可以从简单的图形入手进行总结,然后得到一般化结论再进行求解.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:填空题
 如图,A($\sqrt{3}$,1),B(1,$\sqrt{3}$).将△AOB绕点O旋转150°得到△A′OB′,则此时点A的对应点A′的坐标为(-1,-$\sqrt{3}$)或(-2,0).
如图,A($\sqrt{3}$,1),B(1,$\sqrt{3}$).将△AOB绕点O旋转150°得到△A′OB′,则此时点A的对应点A′的坐标为(-1,-$\sqrt{3}$)或(-2,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 月费/元 | 限定游泳时间/h | 超时费(元/h) | |
| 方式一 | 150 | 30 | 10 |
| 方式二 | 240 | 45 | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
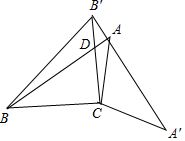 △ABC中,∠ABC=30°,AC=$\sqrt{7}$,BC=2$\sqrt{3}$,将△ABC绕着点C顺时针旋转,A、B两点的对应点分别为A′,B′,若A′,B′刚好经过点A,AB,B′C交于点D,则$\frac{AD}{DB}$=$\frac{7}{48}$.
△ABC中,∠ABC=30°,AC=$\sqrt{7}$,BC=2$\sqrt{3}$,将△ABC绕着点C顺时针旋转,A、B两点的对应点分别为A′,B′,若A′,B′刚好经过点A,AB,B′C交于点D,则$\frac{AD}{DB}$=$\frac{7}{48}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,已知抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C,抛物线的顶点为M,直线BC的解析式为y=x-3.
如图,在平面直角坐标系中,已知抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C,抛物线的顶点为M,直线BC的解析式为y=x-3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com