
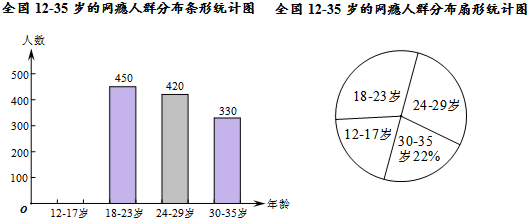
分析 (1)根据30-35岁的人数除以所占的百分比,可得调查的人数;
(2)根据有理数的减法,可得12-17岁的人数,根据12-17岁的人数,可得答案;
(3)根据18-23岁的人数除以抽查的人数乘以360°,可得答案;
(4)根据总人数乘以12-23岁的人数所占的百分比,可得答案.
解答 解:(1)这次抽样调查中共调查了330÷22%=1500(人);
(2)12-17岁的人数为1500-450-420-330=300(人)
补充完整,如图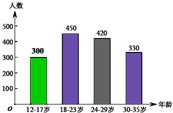 ;
;
(3)扇形统计图中18-23岁部分的圆心角的度数是$\frac{450}{1500}$×360°=108°;
(4)其中12-23岁的人数 2000×50%=1000(万人).
点评 本题考查了条形统计图,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一个抽奖活动的中奖率是5%,则抽100次奖一定会中奖5次 | |
| B. | 了解某批炮弹的杀伤半径,采取普查方式 | |
| C. | 一组数据1、2、3、4的中位数是2.5 | |
| D. | 若甲组数据的方差是S甲2=0.1,乙组数据的方差是S乙2=0.01,则甲组数据比乙组数据稳定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 用笔数(支) | 4 | 5 | 6 | 8 | 9 |
| 学生数 | 4 | 4 | 7 | 3 | 2 |
| A. | 众数是7支 | B. | 中位数是6 | C. | 平均数是5支 | D. | 方差为0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com