
【题目】如图所示,梯形ABCD中,AB∥DC,∠B=90°,AD=15,AB=16,BC=12,点E是边AB上的动点,点F是射线CD上一点,射线ED和射线AF交于点G,且∠AGE=∠DAB.
(1)求线段CD的长;
(2)如果△AEC是以EG为腰的等腰三角形,求线段AE的长;
(3)如果点F在边CD上(不与点C、D重合),设AE=x,DF=y,求y关于x的函数解析式,并写出x的取值范围.

【答案】(1)7;(2)15或![]() ;(3)
;(3)![]() (
(![]() ).
).
【解析】
试题分析:(1)作DH⊥AB于H,如图1,易得四边形BCDH为矩形,则DH=BC=12,CD=BH,再利用勾股定理计算出AH,从而得到BH和CD的长;
(2)分类讨论:当EA=EG时,则∠AGE=∠GAE,则判断G点与D点重合,即ED=EA,作EM⊥AD于M,如图1,则AM=![]() AD=
AD=![]() ,通过证明Rt△AME∽Rt△AHD,利用相似比可计算出此时的AE长;当GA=GE时,则∠AGE=∠AEG,可证明AE=AD=15,(3)作DH⊥AB于H,如图2,则AH=9,HE=AE﹣AH=x﹣9,先利用勾股定理表示出DE=
,通过证明Rt△AME∽Rt△AHD,利用相似比可计算出此时的AE长;当GA=GE时,则∠AGE=∠AEG,可证明AE=AD=15,(3)作DH⊥AB于H,如图2,则AH=9,HE=AE﹣AH=x﹣9,先利用勾股定理表示出DE=![]() ,再证明△EAG∽△EDA,则利用相似比可表示出EG=
,再证明△EAG∽△EDA,则利用相似比可表示出EG=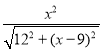 ,则可表示出DG,然后证明△DGF∽△EGA,于是利用相似比可表示出x和y的关系.
,则可表示出DG,然后证明△DGF∽△EGA,于是利用相似比可表示出x和y的关系.
试题解析:(1)作DH⊥AB于H,如图1,易得四边形BCDH为矩形,∴DH=BC=12,CD=BH,在Rt△ADH中,AH=![]() =
=![]() =9,∴BH=AB﹣AH=16﹣9=7,∴CD=7;
=9,∴BH=AB﹣AH=16﹣9=7,∴CD=7;
(2)当EA=EG时,则∠AGE=∠GAE,∵∠AGE=∠DAB,∴∠GAE=∠DAB,∴G点与D点重合,即ED=EA,作EM⊥AD于M,如图1,则AM=![]() AD=
AD=![]() ,∵∠MAE=∠HAD,∴Rt△AME∽Rt△AHD,∴AE:AD=AM:AH,即AE:15=
,∵∠MAE=∠HAD,∴Rt△AME∽Rt△AHD,∴AE:AD=AM:AH,即AE:15=![]() :9,解得AE=
:9,解得AE=![]() ;
;
当GA=GE时,则∠AGE=∠AEG,∵∠AGE=∠DAB,而∠AGE=∠ADG+∠DAG,∠DAB=∠GAE+∠DAG,∴∠GAE=∠ADG,∴∠AEG=∠ADG,∴AE=AD=15,综上所述,△AEC是以EG为腰的等腰三角形时,线段AE的长为![]() 或15;
或15;
(3)作DH⊥AB于H,如图2,则AH=9,HE=AE﹣AH=x﹣9,在Rt△ADE中,DE=![]() =
=![]() ,∵∠AGE=∠DAB,∠AEG=∠DEA,∴△EAG∽△EDA,∴EG:AE=AE:ED,即EG:x=x:
,∵∠AGE=∠DAB,∠AEG=∠DEA,∴△EAG∽△EDA,∴EG:AE=AE:ED,即EG:x=x:![]() ,∴EG=
,∴EG=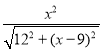 ,∴DG=DE﹣EG=
,∴DG=DE﹣EG=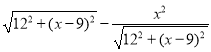 ,∵DF∥AE,∴△DGF∽△EGA,∴DF:AE=DG:EG,即y:x=(
,∵DF∥AE,∴△DGF∽△EGA,∴DF:AE=DG:EG,即y:x=(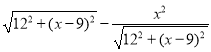 ):
):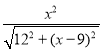 ,∴
,∴![]() (9<x<
(9<x<![]() ).
).



 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
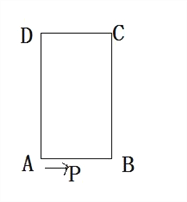
【题目】如图,长方形ABCD中,AB=4cm,BC=6cm,现有一动点P从A出发以2cm/秒的速度,沿矩形的边A—B—C—D回到点A,设点P的运动时间为t秒。
(1)当t=3秒时,求△ABP的面积;
(2)当t为何值时,点P与点A的距离为5cm?
(3)当t为何值时(2<t<5),以线段AD、CP、AP的长度为三角形是直角三角形,且AP是斜边。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种西装和领带,西装每套定价200元,领带每条定价40元.国庆节期间商场决定开展促销活动,活动期间向客户提供两种优惠方案:
方案一:买一套西装送一条领带;
方案二:西装和领带都按定价的90%付款.
现某客户要到该商场购买西装20套,领带x![]() .
.
(1)若该客户按方案一购买,需付款多少元(用含x的式子表示)?若该客户按方案二购买,需付款多少元(用含x的式子表示)?
(2)若![]() ,通过计算说明此时按哪种方案购买较为合算;
,通过计算说明此时按哪种方案购买较为合算;
(3)当![]() 时,你能给出一种更为省钱的购买方法吗?试写出你的购买方法和所需费用.
时,你能给出一种更为省钱的购买方法吗?试写出你的购买方法和所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在一条东西向的双轨铁路上迎面驶来一快一慢两列火车,快车长AB=2(单位长度),慢车长CD=4(单位长度),设正在行驶途中的某一时刻,如图,以两车之间的某点O为原点,取向右方向为正方向画数轴,此时快车头A在数轴上表示的数是a,慢车头C在数轴上表示的数是c,且|a+8|与(c﹣16)2互为相反数.
温馨提示:忽略两辆火车的车身及双铁轨的宽度.

(1)求此时刻快车头A与慢车头C之间相距 单位长度.
(2)从此时刻开始,若快车AB以6个单位长度/秒的速度向右匀速继续行驶,同时慢车CD以2个单位长度/秒的速度向左匀速继续行驶,再行驶 秒两列火车的车头A、C相距8个单位长度.
(3)在(2)中快车、慢车速度不变的情况下,此时在快车AB上有一位爱动脑筋的七年级学生乘客P,他发现行驶中有一段时间t秒钟內,他的位置P到两列火车头A、C的距离和加上到两列火车尾B、D的距离和是一个不变的值(即PA+PC+PB+PD为定值).则这段时间t是 秒,定值是 单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,求作一点P,使P到∠A的两边的距离相等,且PA=PB.下列确定P点的方法正确的是( )
A.P为∠A与∠B的平分线的交点
B.P为∠A的平分线与AB的垂直平分线的交点
C.P为AC,AB两边上的高的交点
D.P为AC,AB两边的垂直平分线的交点
查看答案和解析>>
科目:初中数学 来源: 题型:
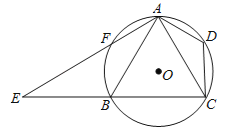
【题目】如图,已知四边形ABCD内接于⊙O,A是![]() 的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F、E,且
的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F、E,且![]() .
.
(1)求证:△ADC∽△EBA;
(2)如果AB=8,CD=5,求tan∠CAD的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com