
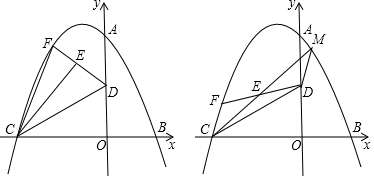
���� ��1����������ó�B�����꣬�������ô���ϵ���������������ʽ��
��2���������ֱ��DC�Ľ���ʽ������ʾ��FP�ij����ٱ�ʾ��S��CEF�������ó�E�����ꣻ
��3�����������ʾ��M�����꣬����������κ�������ʽ�ó�m��ֵ�����ɵó��𰸣�
���  �⣺��1����OA=8��
�⣺��1����OA=8��
��OB=$\frac{1}{2}$OA=4��
��B��4��0����
��y=-$\frac{1}{4}$x2+bx+c��ͼ�����A��0��8����B��4��0����
��$\left\{\begin{array}{l}{-\frac{1}{4}��{4}^{2}+4b+c=0}\\{c=8}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{b=-1}\\{c=8}\end{array}\right.$��
����κ�������ʽΪ��y=-$\frac{1}{4}$x2-x+8��
��2����y=0ʱ��-$\frac{1}{4}$x2-x+8=0��
��ã�x1=4��x2=-8��
��C����������-8��0����
��D����������0��4����
����CD�Ľ���Ϊ��y=kx+d��
��$\left\{\begin{array}{l}{-8k+d=0}\\{d=4}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{d=4}\end{array}\right.$��
��ֱ��DC�Ľ���Ϊ��y=$\frac{1}{2}$x+4��
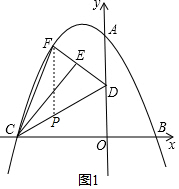
��ͼ1������F��y���ƽ���߽�DC�ڵ�P��
��F����������m��-$\frac{1}{4}$m2-m+8������P����������m��$\frac{1}{2}$m+4����
��FP=-$\frac{1}{4}$m2-$\frac{3}{2}$m+4��
��S��FCP=$\frac{1}{2}$•FP•OC=$\frac{1}{2}$����-$\frac{1}{4}$m2-$\frac{3}{2}$m+4����8
=-m2-6m+16��
��EΪFD�е㣬
��S��CEF=$\frac{1}{2}$��S��FCD=-$\frac{1}{2}$m2-3m+8=-$\frac{1}{2}$��m-3��2+$\frac{25}{2}$��
��m=-3ʱ��S��CEF�����ֵ��
��-$\frac{1}{4}$m2-m+8=-$\frac{1}{4}$��9+3+8=$\frac{35}{4}$��
E����������$\frac{1}{2}$����$\frac{35}{4}$-4��+4=$\frac{51}{8}$��
��F��-3��$\frac{35}{4}$����
��E��-$\frac{3}{2}$��$\frac{51}{8}$����
��3����ͼ2����F������Ϊ����m��-$\frac{1}{4}$m2-m+8����
C����������-8��0����D����������0��4����
��M��m+8��-$\frac{1}{4}$m2-m+12����
�֡�M�����������ϣ�
��-$\frac{1}{4}$��m+8��2-��m+8��+8=-$\frac{1}{4}$m2-m+12��
��ã�m=-7��
��S��CEF=-$\frac{1}{2}$m2-3m+8=$\frac{9}{2}$��
���� ������Ҫ�����˶��κ����ۺ��Լ�����������ʹ���ϵ������������ʽ��֪ʶ����ȷ��ʾ�����������ǽ���ؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | sin60��=$\frac{\sqrt{2}}{2}$ | B�� | a6��a2=a3 | C�� | ��-2��0=2 | D�� | ��2a2b��3=8a6b3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ�У�A��1��3����B��-2��0����C��2��-4����һ��ֱ�������εĶ��㣮
��ͼ�У�A��1��3����B��-2��0����C��2��-4����һ��ֱ�������εĶ��㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6�ĵ��� | B�� | 6���෴�� | C�� | -6�ľ���ֵ | D�� | -6�ĵ��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\overrightarrow{a}$+$\overrightarrow{b}$ | B�� | $\overrightarrow{a}$-$\overrightarrow{b}$ | C�� | -$\overrightarrow{a}$+$\overrightarrow{b}$ | D�� | -$\overrightarrow{a}$-$\overrightarrow{b}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
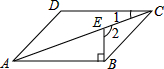 ��ͼ����?ABCD�У�BE��AB���Խ���AC�ڵ�E������1=18�㣬���2=��������
��ͼ����?ABCD�У�BE��AB���Խ���AC�ڵ�E������1=18�㣬���2=��������| A�� | 98�� | B�� | 102�� | C�� | 108�� | D�� | 118�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
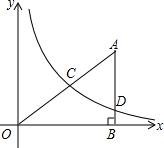 ��ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��ABO�ı�AB��ֱ��x�ᣬ����Ϊ��B������������y=$\frac{k}{x}$��x��0����ͼ��AO�ϵĵ�C����$\frac{OC}{OA}=\frac{2}{3}$����AB�ཻ�ڵ�D��OB=6��AD=$\frac{5}{2}$��
��ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��ABO�ı�AB��ֱ��x�ᣬ����Ϊ��B������������y=$\frac{k}{x}$��x��0����ͼ��AO�ϵĵ�C����$\frac{OC}{OA}=\frac{2}{3}$����AB�ཻ�ڵ�D��OB=6��AD=$\frac{5}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
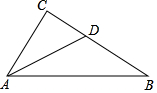 ��ͼ��Rt��ABC�У���C=90�㣬ADƽ�֡�BAC��BC��D����BC=16��CD=6����AC=12��
��ͼ��Rt��ABC�У���C=90�㣬ADƽ�֡�BAC��BC��D����BC=16��CD=6����AC=12���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com