
 如图,是用棋子摆成的图形,按照这种摆法,第n个图形中所需棋子的总数是用了n(n+1)个.
如图,是用棋子摆成的图形,按照这种摆法,第n个图形中所需棋子的总数是用了n(n+1)个.  53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:选择题
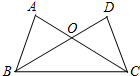 如图,已知∠ABC=∠BCD,则下列条件中,不能作为判定△ABC≌△DCB的是( )
如图,已知∠ABC=∠BCD,则下列条件中,不能作为判定△ABC≌△DCB的是( )| A. | ∠A=∠D | B. | ∠ACB=∠DBC | C. | AB=DC | D. | AC=DB |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
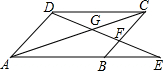 如图,AC是平行四边形ABCD的对角线,DE与AB的延长线交于点E,与BC交于点F,与AC交于点G,则图中有相似三角形( )
如图,AC是平行四边形ABCD的对角线,DE与AB的延长线交于点E,与BC交于点F,与AC交于点G,则图中有相似三角形( )| A. | 3对 | B. | 4对 | C. | 5对 | D. | 6对 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
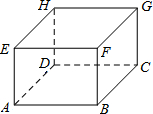 如图,在长方体ABCD-EFGH中,可以把平面ABFE与平面BCGF组成的图形看作直立于面ABCD上的合页形折纸,从而说明棱BF垂直于平面ABCD.
如图,在长方体ABCD-EFGH中,可以把平面ABFE与平面BCGF组成的图形看作直立于面ABCD上的合页形折纸,从而说明棱BF垂直于平面ABCD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
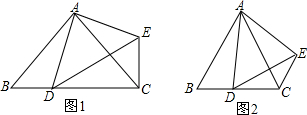 在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
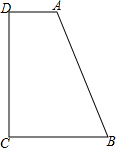 如图,在梯形ABCD中,AD∥BC,∠D=90°,DC=6,AD=2,BC=4,如果在边DC上找一点P使得△PAD和△PBC相似,那么这样的点P存在的个数是( )
如图,在梯形ABCD中,AD∥BC,∠D=90°,DC=6,AD=2,BC=4,如果在边DC上找一点P使得△PAD和△PBC相似,那么这样的点P存在的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)解不等式,3(x-1)-5x≤1,并把解集表示在数轴上.
(1)解不等式,3(x-1)-5x≤1,并把解集表示在数轴上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com