
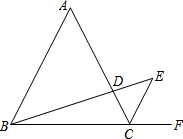
 (2013•崇明县一模)如图,△ABC是等边三角形,且AD•ED=BD•CD.
(2013•崇明县一模)如图,△ABC是等边三角形,且AD•ED=BD•CD.| AD |
| CD |
| BD |
| DE |
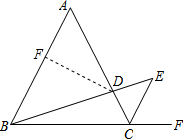 (1)证明:∵AD•ED=BD•CD,
(1)证明:∵AD•ED=BD•CD,| AD |
| CD |
| BD |
| DE |
| CD |
| AD |
| DE |
| BD |
| 1 |
| 2 |
| 2 |
| 3 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| BF2+DF2 |
42+(2
|
| 7 |
| CD |
| AD |
| DE |
| BD |
| 1 |
| 2 |
| 7 |
| 7 |
| 7 |


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•崇明县一模)如图,在航线l的两侧分别有观测点A和B,点A到航线l的距离为2海里,点B位于点A北偏东60°方向且与A相距l0海里处.现有一艘轮船从位于点B南偏西76°方向的C处,正沿该航线自西向东航行,10分钟后该轮船行至点A的正北方向的D处.
(2013•崇明县一模)如图,在航线l的两侧分别有观测点A和B,点A到航线l的距离为2海里,点B位于点A北偏东60°方向且与A相距l0海里处.现有一艘轮船从位于点B南偏西76°方向的C处,正沿该航线自西向东航行,10分钟后该轮船行至点A的正北方向的D处.| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com