
 如图,在△ABC中,∠ACB=90°,AB=10,cosB=$\frac{3}{5}$,G为BC上一点(不与B重合),以BG为直径的圆O交AB于D,作AD的垂直平分线交AD于F,交AC于E,连结DE.
如图,在△ABC中,∠ACB=90°,AB=10,cosB=$\frac{3}{5}$,G为BC上一点(不与B重合),以BG为直径的圆O交AB于D,作AD的垂直平分线交AD于F,交AC于E,连结DE.分析 (1)连接OD、DG,由BG为圆的直径可知∠BDG是直角,然后只要证明∠ODE=90°,即可证明结论成立,根据题目中的条件可以得到∠ODE=90°,本题得以解决;
(2)根据题目中的条件和勾股定理,可以转化为直角三角形ODE和直角三角形OCD两直角边的平方等于OE的平方,从而可以得到DE的长;
(3)根据(2)中的求解方法,可以得到y与x的函数关系式,根据一次函数的性质,可以得到y的最小值.
解答  (1)证明:连接OD、DG,如右图所示,
(1)证明:连接OD、DG,如右图所示,
∵BG为⊙O的直径,OD=OB,∠ACB=90°,
∴∠BDG=90°,∠ODB=∠B,∠B+∠A=90°,
∴∠A=∠ODG,∠GDE+∠EDA=90°,
又∵EF是AD的垂直平分线,
∴∠A=∠EDA,
∴∠EDA=∠ODG,
∴∠GDE+∠ODG=90°,
即OD⊥DE,
∵OD是⊙O的半径,
∴DE为⊙O的切线;
(2)连接OE,如右上图所示,
∵∠ACB=90°,AB=10,cosB=$\frac{3}{5}$,
∴BC=AB•cosB=6,AC=$\sqrt{A{B}^{2}-B{C}^{2}}=8$,
∵BG=3,
∴OD=1.5,OC=BC-OB=6-1.5=4.5,
∵EF是AD的垂直平分线,
∴EA=ED,
设EA=x,则ED=x,EC=8-x,
∵∠ECO=90°,∠EDO=90°,
∴DE2+OD2=EC2+OC2,
即x2+1.52=(8-x)2+4.52,
解得,x=$\frac{41}{8}$,
即DE的长是$\frac{41}{8}$;
(3)连接OE,如右上图所示,
∵∠ACB=90°,AB=10,cosB=$\frac{3}{5}$,
∴BC=AB•cosB=6,AC=$\sqrt{A{B}^{2}-B{C}^{2}}=8$,
∵BG=x,
∴OD=0.5x,OC=BC-OB=6-0.5x,
∵EF是AD的垂直平分线,ED=y,
∴EA=ED=y,
∴EC=8-y,
∵∠ECO=90°,∠EDO=90°,
∴DE2+OD2=EC2+OC2,
即y2+(0.5x)2=(8-y)2+(6-0.5x)2,
化简,得y=$-\frac{3}{8}x+\frac{50}{8}$,(0<x≤6)
∵-$\frac{3}{8}$<0,
∴y随x的增大而减小,
∴当x=6时,y取得最小值,此时y=$-\frac{3}{8}×6+\frac{50}{8}$=4,
即y与x的函数关系是y=$-\frac{3}{8}x+\frac{50}{8}$,(0<x≤6),y的最小值是4.
点评 本题考查圆的综合题,解题的关键是明确题意,找出所求问题需要的条件,作出合适的辅助线,利用数形结合的思想解答问题.


 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
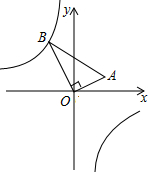 如图,在△AOB中,∠AOB=90°,点A的坐标为(2,1),BO=2$\sqrt{5}$,反比例函数y=$\frac{k}{x}$的图象经过点B,则k的值为-8.
如图,在△AOB中,∠AOB=90°,点A的坐标为(2,1),BO=2$\sqrt{5}$,反比例函数y=$\frac{k}{x}$的图象经过点B,则k的值为-8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
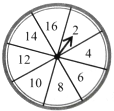 如图,一个均匀的转盘被平均分成8等份,分别标有2,4,6,8,10,12,14,16这8个数字.转动转盘,当转盘停止后,指针指向的数字即为转出的数字.小亮与小颖参与游戏:小亮转动转盘,小颖猜数,若所猜数字与转出的数字相符,则小颖获胜,否则小亮获胜.
如图,一个均匀的转盘被平均分成8等份,分别标有2,4,6,8,10,12,14,16这8个数字.转动转盘,当转盘停止后,指针指向的数字即为转出的数字.小亮与小颖参与游戏:小亮转动转盘,小颖猜数,若所猜数字与转出的数字相符,则小颖获胜,否则小亮获胜.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com