
������������ת����Ϸʱ����ת��A��B�ֱ�ֳ�4�ȷݡ�3�ȷݣ�����ÿһ���ڱ������֣���ͼ��ʾ����Ϸ�涨��ת������ת��ֹͣ��ָ�����ָ��ijһ���֣�������ת��
��1��������״ͼ���б����г����п��ܵĽ����
��2����ָ����ָ���������ֶ��Ƿ���x2-5x+6=0�Ľ�ʱ�����ʤ����ָ����ָ���������ֶ����Ƿ���x2-5x+6=0�Ľ�ʱ�����һ�ʤ������������˭��ʤ�ĸ��ʴ������˵����

 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д� �ۺ��Բ�ϵ�д�
�ۺ��Բ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����꼶��ѧ��ʦ����ϲ��3�� ��ʽ����Ӽ� ��Ԫ���Ծ� ���ͣ������
һ��������һ���߳�Ϊa��b����һ���߱������߳�2a��b���������߱������߶�3a��b������������ε��ܳ�Ϊ____________��
2a��5b ����������һ��������һ�߳�Ϊa+b����һ�߱������߳�2a+b�� ����һ�߳�Ϊ��a+b+2a+b=3a+2b�� �ߵ������߱������߶�3a-b�� ��������߳�Ϊ��a+b-��3a-b��=2b-2a�� ������������ε��ܳ�=��a+b��+��3a+2b��+��2b-2a��=2a+5b�� �ʴ��ǣ�2a+5b.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ��ɽ��ʡ��������У���꼶���ϣ���һ��������ѧ�Ծ� ���ͣ������
ijУ������У�������У������ѧ����ȥ���Σ���������˵����У����ȫƱһ�ţ���ѧ����ۣ�����������˵��ȫ���������Żݡ���ȫƱ����1200Ԫ����
��1����ѧ��������20�ˣ��ס����������շѷֱ��Ƕ��٣�
��2����ѧ�������Ķ���ʱ��������������շ�һ����
��1�����������շ���13200Ԫ�����������շ���15120Ԫ����2��4�� ����������������� ��1���������������ݸ��ݼס�����������Ե��Żݷ������м��㼴�ɣ� ��2����ѧ������Ϊ�����ʱ����������շ�Ϊ��Ԫ������������շ�Ϊ��Ԫ������������������շ�һ�������г����̣��ⷽ�̼�����������. ��������� ��1����ѧ������Ϊ20��ʱ�� ����������շ�Ϊ��1200+...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ��ɽ��ʡ��������У���꼶���ϣ���һ��������ѧ�Ծ� ���ͣ���ѡ��
һ���칫������5յ�ƣ�������40W��60W���ֵ��ݣ��ܵ�����Ϊ260W����40W��60W�ĵ��ݸ����ֱ�Ϊ�� ��
A. 1��4 B. 2��3 C. 3��2 D. 4��1
B ����������40w�ĵ����и���������ɵã� �� ��ã� �� �࣬ ��40w�ĵ�����2����60w�ĵ�����3��. ��ѡB.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ����ѧ����ĩ��ѧ���������꼶��ѧ�Ծ� ���ͣ������
һ��ֱ��������ľ�壬����һ��ֱ�DZ�AB��1.5m�����Ϊ1.5m2���ס�����λľ���ֱ�ͼ�١��ڰ����ӹ���һ�����������森��˵���ĸ�����������ϴӹ���IJ��ƣ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ����ѧ����ĩ��ѧ���������꼶��ѧ�Ծ� ���ͣ���ѡ��
ij��Ϊ�������������ƻ�����ͼ��ʾ�������οյ�����ֲ��Ƥ����֪���ֲ�Ƥÿƽ�����ۼ�ΪaԪ���������ֲ�Ƥ������Ҫ��������

A. 450aԪ B. 225aԪ C. 150aԪ D. 300aԪ
C �������������������ͼ����BA�ߵĸ�CD������BA���ӳ��߽��ڵ�D�� �ߡ�BAC=150�㣬 ���DAC=30�㣬 ��CD��BD��AC=30m�� ��CD=15m�� ��AB=20m�� ��S��ABC=AB��CD=��20��15=150m2�� ��ÿƽ�����ۼ�aԪ�� ������ֲ�Ƥ�ļ۸�Ϊ150aԪ�� ��ѡC.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ����ѧ����ĩ��ѧ���������꼶��ѧ�Ծ� ���ͣ������
��ͼ�����߳�Ϊ6cm��������ABCD�۵���ʹ��D����AB�ߵ��е�E�����ۺ�ΪFH����C����Q����EQ��BC���ڵ�G�����EBG���ܳ��� cm��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2018����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
��ͼ��  ��
�� ��˫�����ϵ����㣬��
��˫�����ϵ����㣬��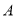 ����
����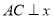 ���ڵ�
���ڵ� ����
���� �ڵ�
�ڵ� ����
���� �����Ϊ
�����Ϊ ��
�� 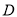 Ϊ
Ϊ ���е㣬��
���е㣬��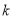 ��ֵΪ__________��
��ֵΪ__________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�������ʡ��������˫�������꼶���ϣ���ĩ��ѧ�Ծ�������ѧ�ƣ� ���ͣ������
ij���й涨�����������50Ԫ����Ʒʱ����ȫ���շѣ�����50Ԫ����Ʒʱ���������ְ������շѣ�ij�˿���һ�������У����ۻ�Ա������212Ԫ����ô�ڴ˴������иù˿����˼�ֵ Ԫ����Ʒ��
230 �������������������������Ʒ�ļ�ֵΪxԪ�����ݽ��ɵ�Ǯ���г����̽������.������з���Ϊ50+��x��50����90%=212����ã�x=230.�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com