
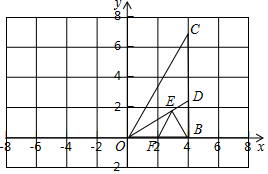
 如图,Rt△OBC中,OB=4,∠BOC=60°,∠BOC的平分线交BC于D,E、F分别是OD、OB上的动点,BE+EF取到最小值时,E点坐标为(2,$\frac{2\sqrt{3}}{3}$).
如图,Rt△OBC中,OB=4,∠BOC=60°,∠BOC的平分线交BC于D,E、F分别是OD、OB上的动点,BE+EF取到最小值时,E点坐标为(2,$\frac{2\sqrt{3}}{3}$). 分析 作B关于直线OD的对称点A,过A作AF⊥OB交OD于E,则AF的长度=BE+EF的最小值,根据已知条件得到△AOB是等边三角形,根据的比较熟悉的性质得到OA=OB=4,OF=$\frac{1}{2}$OB=2,由角平分线的定义得到∠EOF=30°,解直角三角形即可得到结论.
解答 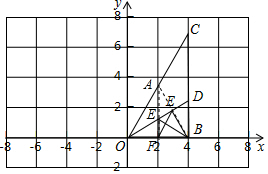 解:作B关于直线OD的对称点A,过A作AF⊥OB交OD于E,
解:作B关于直线OD的对称点A,过A作AF⊥OB交OD于E,
则AF的长度=BE+EF的最小值,
∵∠BOC=60°,
∴△AOB是等边三角形,
∴OA=OB=4,OF=$\frac{1}{2}$OB=2,
∵OD 是∠AOB的平分线,
∴∠EOF=30°,
∴EF=$\frac{\sqrt{3}}{3}$OF=$\frac{2\sqrt{3}}{3}$,
∴E(2,$\frac{2\sqrt{3}}{3}$).
故答案为:(2,$\frac{2\sqrt{3}}{3}$).
点评 本题考查了轴对称-最短路线问题,等边三角形的判定和性质,坐标与图形的性质,解题的关键是正确的作出对称点.


科目:初中数学 来源: 题型:选择题
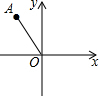 如图,在平面直角坐标系中,点A的坐标为(-1,$\sqrt{3}$),以原点O为中心,将点A顺时针旋转150°得到点A′,则点A′的坐标为( )
如图,在平面直角坐标系中,点A的坐标为(-1,$\sqrt{3}$),以原点O为中心,将点A顺时针旋转150°得到点A′,则点A′的坐标为( )| A. | (0,-2) | B. | (1,-$\sqrt{3}$) | C. | (2,0) | D. | ($\sqrt{3}$,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 景区 | 潜山公园 | 陆水湖 | 隐水洞 | 三湖连江 |
| 气温 | -1℃ | 0℃ | -2℃ | 2℃ |
| A. | 潜山公园 | B. | 陆水湖 | C. | 隐水洞 | D. | 三湖连江 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
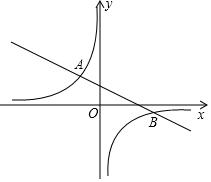 如图,已知点 A(-2,m+4),点B(6,m)在反比例函数y=$\frac{k}{x}$(k≠0)的图象上.
如图,已知点 A(-2,m+4),点B(6,m)在反比例函数y=$\frac{k}{x}$(k≠0)的图象上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
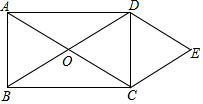 如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.
如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com