
【题目】已知如图,BQ平分∠ABP,CQ平分∠ACP,∠BAC=α,∠BPC=β,则∠BQC=_________.(用α,β表示)

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在一次数学课上,李老师让同学们独立完成课本第23页第七题选择题(2)如图 1,如果 AB∥CD∥EF,那么∠BAC+∠ACE+∠CEF=( )
A.180° B.270° C.360° D.540°
(1)请写出这道题的正确选项;
(2)在同学们都正确解答这道题后,李老师对这道题进行了改编:如图2,AB∥EF,请直接写出∠BAD,∠ADE,∠DEF之间的数量关系.
(3)善于思考的龙洋同学想:将图1平移至与图2重合(如图3所示),当AD,ED分别平分∠BAC,∠CEF时,∠ACE与∠ADE之间有怎样的数量关系?请你直接写出结果,不需要证明.
(4)彭敏同学又提出来了,如果像图4这样,AB∥EF,当∠ACD=90°时,∠BAC、∠CDE和∠DEF之间又有怎样的数量关系?请你直接写出结果,不需要证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A、B、C是数轴上的三点,点C表示的数是6,点B与点C之间的距离是4,点B与点A的距离是12,点P为数轴上一动点.
(1)数轴上点A表示的数为 .点B表示的数为 ;
(2)数轴上是否存在一点P,使点P到点A、点B的距离和为16,若存在,请求出此时点P所表示的数;若不存在,请说明理由;
(3)点P以每秒1个单位长度的速度从C点向左运动,点Q以每秒2个单位长度从点B出发向左运动,点R从点A以每秒5个单位长度的速度向右运动,它们同时出发,运动的时间为t秒,请求点P与点Q,点R的距离相等时t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】补全解答过程:
已知:如图,直线![]() ,直线
,直线![]() 与直线
与直线![]() ,
,![]() 分别交于点
分别交于点![]() ,
,![]() ;
;![]() 平分
平分![]() ,
,![]() .求
.求![]() 的度数.
的度数.

解:![]() 与
与![]() 交于点
交于点![]() ,(已知)
,(已知)
![]() .(_______________)
.(_______________)
![]() ,(已知)
,(已知)
![]() .(______________)
.(______________)
![]() ,
,![]() 与
与![]() ,
,![]() 交于点
交于点![]() ,
,![]() ,(已知)
,(已知)
![]() (_____________)
(_____________)
![]() _______
_______![]()
![]() 平分
平分![]() ,(已知)
,(已知)
![]() _______
_______![]() .(角平分线的定义)
.(角平分线的定义)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图表示的是热带风暴从发生到结束的全过程,请结合图象回答下列问题:

(1)热带风暴从开始发生到结束共经历了 个小时;
(2)从图象上看,风速在 (小时)时间段内增大的最快?最大风速是 千米/时;
(3)风速从开始减小到最终停止,平均每小时减小多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过△ABC的三个顶点,与y轴相交于(0, ![]() ),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
(1)求该抛物线的函数解析式;
(2)点F为线段AC上一动点,过点F作FE⊥x轴,FG⊥y轴,垂足分别为点E,G,当四边形OEFG为正方形时,求出点F的坐标;
(3)将(2)中的正方形OEFG沿OC向右平移,记平移中的正方形OEFG为正方形DEFG,当点E和点C重合时停止运动,设平移的距离为t,正方形的边EF与AC交于点M,DG所在的直线与AC交于点N,连接DM,是否存在这样的t,使△DMN是等腰三角形?若存在,求t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图 1,AB∥CD,直线 EF 交 AB 于点 E,交 CD 于点 F,点 G 在 CD 上,点 P在直线 EF 左侧,且在直线 AB 和 CD 之间,连接 PE,PG.
(1) 求证: ∠EPG=∠AEP+∠PGC;
(2) 连接 EG,若 EG 平分∠PEF,∠AEP+ ∠ PGE=110°,∠PGC=![]() ∠EFC,求∠AEP 的度数.
∠EFC,求∠AEP 的度数.
(3) 如图 2,若 EF 平分∠PEB,∠PGC 的平分线所在的直线与 EF 相交于点 H,则∠EPG 与∠EHG之间的数量关系为 .
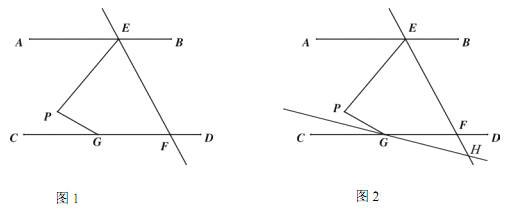
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线经过A(﹣4,0),B(0,﹣4),C(2,0)三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)﹣2a3b(﹣4a2b)÷6a4b2
(2)![]()
(3)![]()
(4)(2a﹣1)(a﹣4)﹣(a+3)(a﹣4)
(5)(x﹣3y+4)(x+3y﹣4)
(6)(a+2b)(a﹣2b)(a2﹣4b2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com