
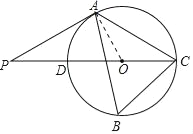
【题目】如图△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若PD=![]() ,求⊙O的直径.
,求⊙O的直径.

【答案】(1)证明见解析;(2)⊙O的直径为2![]() .
.
【解析】
(1)连接OA,根据圆周角定理求出∠AOC,再由OA=OC得出∠ACO=∠OAC=30°,再由AP=AC得出∠P=30°,继而由∠OAP=∠AOC-∠P,可得出OA⊥PA,从而得出结论;
(2)利用含30°的直角三角形的性质求出OP=2OA,可得出OP-PD=OD,再由![]() 可得出⊙O的直径.
可得出⊙O的直径.
(1)证明:连接OA,
∵∠B=60°,
∴∠AOC=2∠B=120°,
又∵OA=OC,
∴∠OAC=∠OCA=30°,
又∵AP=AC,
∴∠P=∠ACP=30°,
∴∠OAP=∠AOC﹣∠P=90°,
∴OA⊥PA,
∴PA是⊙O的切线.
(2)在Rt△OAP中,∵∠P=30°,
∴PO=2OA=OD+PD,
又∵OA=OD,
∴PD=OA,
∵![]()
∴![]()
∴⊙O的直径为![]()


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=110°,点E、G分别是AB、AC的中点,DE⊥AB交BC于D,FG⊥AC交BC于F,连接AD、AF.试求∠DAF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
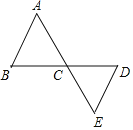
【题目】如图,连接在一起的两个等边三角形的边长都为1cm,一个微型机器人由点A开始按A→B→C→D→E→C→A→B→C…的顺序沿等边三角形的边循环移动.当微型机器人移动了2019cm后,它停在了点_____上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,点D为⊙O上一点,且CD=CB、连接DO并延长交CB的延长线于点E.
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)若BE=4,DE=8,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
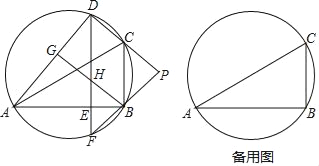
【题目】如图,D是△ABC外接圆上的动点,且B,D位于AC的两侧,DE⊥AB,垂足为E,DE的延长线交此圆于点F.BG⊥AD,垂足为G,BG交DE于点H,DC,FB的延长线交于点P,且PC=PB.
(1)求证:BG∥CD;
(2)设△ABC外接圆的圆心为O,若AB=![]() DH,∠OHD=80°,求∠BDE的大小.
DH,∠OHD=80°,求∠BDE的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形纸片分别沿两条不同的直线剪两刀,可以使剪得的三块纸片恰能拼成一个等腰三角形(不能有重叠和缝隙).小华的做法是:如图1所示,在矩形ABCD中,分别取AD、AB、CD的中点P、E、F,并沿直线PE 、PF剪两刀,所得的三部分可拼成等腰三角形△PMN (如图2).

(1)在图3中画出另一种剪拼成等腰三角形的示意图;
(2)以矩形ABCD的顶点B为原点,BC所在直线为x轴建立平面直角坐标系(如图4),矩形ABCD剪拼后得到等腰三角形△PMN,点P在边AD上(不与点A、D重合),点M、N在x轴上(点M在N的左边).如果点D的坐标为(5,8),直线PM的解析式为y=kx+b,求所有满足条件的k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,已知点A(-1,4),B(-2,2),C(1,1).

(1)作ΔABC关于x轴对称的△A1B1C1,并写出点A1,B1,C1的坐标,
(2)作△ABC关于y轴对称的△A2B2C2,并写出点A2,B2,C2的坐标,
(3)观察点A1,B1,C1和A2,B2,C2的坐标,请用文字语言归纳点A1和A2,B1和B2,C1和C2坐标之间的关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com