
| A. | 正数 | B. | 负数 | C. | 零 | D. | 正数或负数 |
分析 根据题目中的式子,变形即可求得所求式子的正负情况,本题得以解决.
解答 解:∵a+b+c=0,abc=8,
∴(a+b+c)2=0,
∴a2+b2+c2+2ab+2bc+2ac=0,
∴2ab+2bc+2ac=-(a2+b2+c2)
∴$\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{c}$
=$\frac{bc+ac+ab}{abc}$
=$\frac{ab+bc+ac}{8}$
=$\frac{2ab+2bc+2ac}{16}$
=$\frac{-({a}^{2}+{b}^{2}+{c}^{2})}{16}$,
∵abc=8,
∴a、b、c都不是零,
∴-(a2+b2+c2)<0,
∴$\frac{-({a}^{2}+{b}^{2}+{c}^{2})}{16}$<0,
故选B.
点评 本题考查分式的化简求值,解题的关键是明确分式化简求值的方法.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 抛一枚硬币,正面朝上 | |
| B. | 通常加热到100℃,水沸腾 | |
| C. | 明天会下雪 | |
| D. | 经过某一有交通信号灯的路口恰好遇到红灯 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中.直线y=-x+3与x轴交于点B,与y轴交于点C,抛物线y=ax2+bx+c经过B,C两点,与x轴负半轴交于点A,连结AC,tan∠CAB=3
如图,在平面直角坐标系中.直线y=-x+3与x轴交于点B,与y轴交于点C,抛物线y=ax2+bx+c经过B,C两点,与x轴负半轴交于点A,连结AC,tan∠CAB=3查看答案和解析>>
科目:初中数学 来源: 题型:解答题
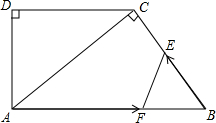 如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).
如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
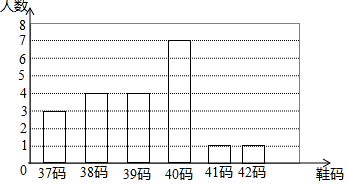 某鞋厂为了了解初中学生穿鞋的鞋号情况,对某中学八年级(1)班的20名男生所穿鞋号进行了调查,结果如图所示
某鞋厂为了了解初中学生穿鞋的鞋号情况,对某中学八年级(1)班的20名男生所穿鞋号进行了调查,结果如图所示查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com