

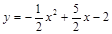 (2)存在!P为(2,1)或(5,-2)或(-3,-14) (3)D(2,1)
(2)存在!P为(2,1)或(5,-2)或(-3,-14) (3)D(2,1) 解之
解之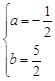
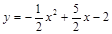 .
.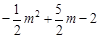 ,
,
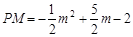 .又∵∠COA=∠PMA=90°,
.又∵∠COA=∠PMA=90°,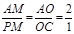 时,△PMA∽△COA,即
时,△PMA∽△COA,即 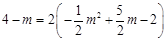 .
.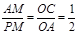 时,△APM∽△CAO,即
时,△APM∽△CAO,即 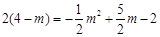 .
.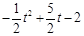 .
.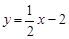 ,
,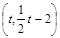 .∴
.∴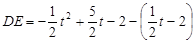 =
=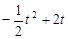
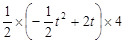 =-t2+4t=-(t-2)2+4.∴当t=2时,△DAC面积最大.∴D(2,1)
=-t2+4t=-(t-2)2+4.∴当t=2时,△DAC面积最大.∴D(2,1)

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源:不详 题型:解答题
 交
交 轴于
轴于 两点,交
两点,交 轴于点
轴于点 ,对称轴为直线
,对称轴为直线 。且A、C两点的坐标分别为
。且A、C两点的坐标分别为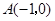 ,
,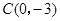 .
.
 的解析式;
的解析式; ,使
,使 的周长最小.若存在,请求出点
的周长最小.若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
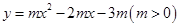 与
与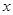 轴交于
轴交于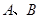 两点,与
两点,与 轴交于
轴交于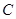 点.
点.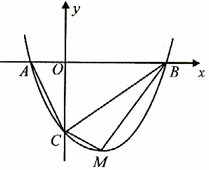
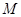 的坐标(用含
的坐标(用含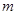 的代数式表示),
的代数式表示),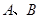 两点的坐标;
两点的坐标;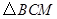 与
与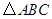 的面积比不变,试求出这个比值;
的面积比不变,试求出这个比值;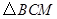 为直角三角形的抛物线?若存在,请求出;如果不存在,请说明理由.
为直角三角形的抛物线?若存在,请求出;如果不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
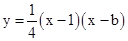 (b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位于点B的左侧),与y轴的正半轴交于点C.
(b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位于点B的左侧),与y轴的正半轴交于点C.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,点A在x轴负半轴上,点B在坐标原点.点D的坐标为(
,点A在x轴负半轴上,点B在坐标原点.点D的坐标为( ,3),抛物线y=ax2+b(a≠0)经过AB、CD两边的中点.
,3),抛物线y=ax2+b(a≠0)经过AB、CD两边的中点.
 )
)查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
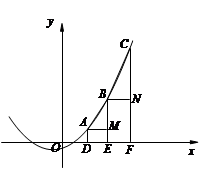
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com