
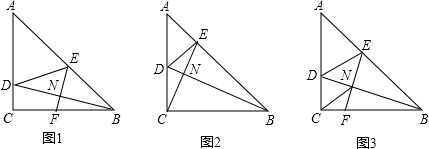
分析 (1)首先证明∠ADE=∠BDC=75°,再证明∠AED=∠BEN=60°,在Rt△DEN中利用30度性质即可解决问题.
(2)如图2中,作AM⊥AC交CE的延长线于M.只要证明△ACM≌△CBD,△AED≌△AEM即可解决问题.
(3)如图3中,连接CN、DF.首先证明△ADE≌△BFE推出AD=BF,CD=CF,将△CFN逆时针旋转90°得到△CDG,只要证明G、D、N共线,△GCN是等腰直角三角形,
即可解决问题.
解答 (1)解:如图1中,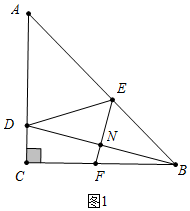
∵AC=BC,∠ACB=90°,
∴∠A=∠ABC=45°,
∵∠DBC=15°,
∴∠BDC=∠ADE=75°,
∵EF⊥BD,
∴∠FNB=90°,∠BFN=75°,
∴∠AED=180°-∠A-∠ADE=60°,∠FEB=180°-∠EBF-∠EFB=60°,
∴∠DEF=180°-∠AED-∠FEB=60°,
∴∠DEN=∠BEN=60°,
∵∠DNE=90°,∠EDN=30°,DE=4,
∴EN=$\frac{1}{2}$DE=2.
(2)证明:如图2中,作AM⊥AC交CE的延长线于M.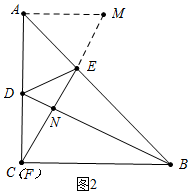
∵∠ACM+∠BCN=80°,∠BCN+∠CBN=90°,
∴∠ACN=∠DBC,
在△ACM和△CBD中,
$\left\{\begin{array}{l}{∠CAM=∠DCB}\\{AC=BC}\\{∠ACM=∠DBC}\end{array}\right.$,
∴△ACM≌△CBD,
∴AM=CD,∠M=∠BDC=∠ADE,
∵∠CAM=90°,∠CAB=45°,
∴∠EAD=∠EAM=45°,
在△EAD和△EAM中,
$\left\{\begin{array}{l}{∠EAD=∠EAM}\\{∠ADE=∠M}\\{AE=AE}\end{array}\right.$,
∴△AED≌△AEM,
∴AD=AM,
∴AD=CD.
(3)证明:如图3中,连接CN、DF.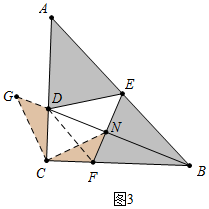
∵∠EFB+∠FBN=90°,∠FBN+∠BDC=90°,
∴∠EFB=∠BDC=∠ADE,
在△ADE和△BFE中,
$\left\{\begin{array}{l}{∠A=∠EBF}\\{∠ADE=∠EFB}\\{AE=EB}\end{array}\right.$,
∴△ADE≌△BFE,
∴AD=BF,
∵AC=CB,
∴CD=CF,将△CFN逆时针旋转90°得到△CDG,
∵∠DCF+∠DNF=180°,
∴∠CDN+∠CFN=180°,
∵∠CFN=∠CDG,
∴∠CDN+∠CDG=180°,
∴G、D、N共线,
∴DN+FN=GN+DG=NG,
∵∠FCN=∠DCG,CN=CG,
∴∠GCN=∠ACB=90°,
∴△GCN是等腰直角三角形,
∴NG=$\sqrt{2}$CD,
∴DN+NF=$\sqrt{2}$CD.
点评 本题考查全等三角形的判定和性质.等腰直角三角形的性质、直角三角形30度角性质等知识,具体的是关键是学会添加常用辅助线构造全等三角形解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
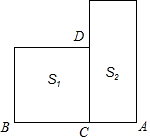 如图,若S1表示以BC为边的正方形面积,S2表示以AB为长、AC为宽的矩形面积,且S1=S2.则图中可看作线段黄金分割点的是( )
如图,若S1表示以BC为边的正方形面积,S2表示以AB为长、AC为宽的矩形面积,且S1=S2.则图中可看作线段黄金分割点的是( )| A. | 点C | B. | 点D | C. | 点C和点D | D. | 没有 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5 cm | B. | 3 cm | C. | 17 cm | D. | 12 cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
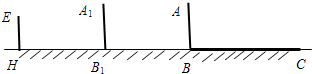 学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为1.6m的小明(AB)的影子BC长是3m,而小颖(EH)刚好在路灯灯泡的正下方H点,并测得HB=6m.
学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为1.6m的小明(AB)的影子BC长是3m,而小颖(EH)刚好在路灯灯泡的正下方H点,并测得HB=6m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com