
 过点P, P点的坐标为(3-m,2m),m是分式方程
过点P, P点的坐标为(3-m,2m),m是分式方程 的解,PA⊥x轴于点A,PB⊥y轴于点B.
的解,PA⊥x轴于点A,PB⊥y轴于点B.

 在第三象限内的一动点,过M作MN⊥x轴于交AB的延长线于点N,是否存在一点M使得四边形OMNB为等腰梯形?若存在,请求出M点的坐标;若不存在,请说明理由.
在第三象限内的一动点,过M作MN⊥x轴于交AB的延长线于点N,是否存在一点M使得四边形OMNB为等腰梯形?若存在,请求出M点的坐标;若不存在,请说明理由.
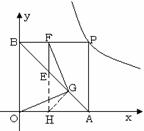


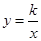 第三象限上一动点
第三象限上一动点

科目:初中数学 来源:不详 题型:解答题
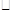 OABC的顶点A, C的坐标分别为A(2,0),C(-1,2),反比例函数
OABC的顶点A, C的坐标分别为A(2,0),C(-1,2),反比例函数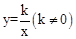 的图像经过点B.
的图像经过点B.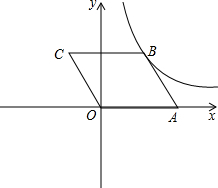
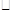 OABC沿着x轴翻折,点C落在点C′处.判断点C′是否在反比例函数
OABC沿着x轴翻折,点C落在点C′处.判断点C′是否在反比例函数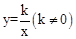 的图像上,请通过计算说明理由.
的图像上,请通过计算说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
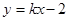 分别交x轴、y轴于点A、B,点P为AB上一点且PC为△AOB的中位线,PC的延长线交反比例函数
分别交x轴、y轴于点A、B,点P为AB上一点且PC为△AOB的中位线,PC的延长线交反比例函数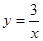 的图象 于点Q,若PQ=
的图象 于点Q,若PQ=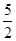 ,求k的值.
,求k的值.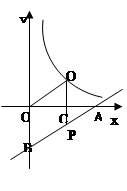
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
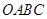 的面积为4,点
的面积为4,点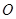 为坐标原点,点
为坐标原点,点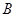 在函数
在函数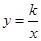 (
(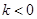 ,
,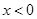 )的图象上,点
)的图象上,点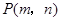 是函数
是函数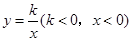 的图象上异于
的图象上异于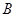 的任意一点,过点
的任意一点,过点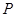 分别作
分别作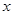 轴,
轴,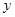 轴的垂线,垂足分别为
轴的垂线,垂足分别为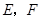 .
.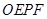 的面积为
的面积为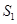 ,判断
,判断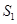 与点
与点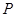 的位置是否有关(不必说理由).
的位置是否有关(不必说理由).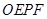 的面积中减去其与正方形
的面积中减去其与正方形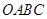 重合的面积,剩余面积记为
重合的面积,剩余面积记为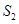 ,写出
,写出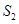 与
与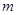 的函数关系,并标明
的函数关系,并标明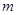 的取值范围.
的取值范围.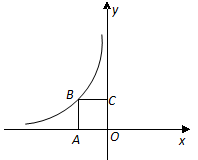
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
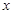 轴正半轴上任意一点,过点M作PQ∥
轴正半轴上任意一点,过点M作PQ∥ 轴,分别交函数
轴,分别交函数 (
(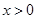 )和
)和 (
(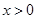 )的图象于点P和Q,连接OP和OQ.则下列结论:
)的图象于点P和Q,连接OP和OQ.则下列结论: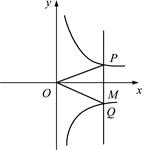
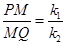 ;
; 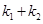 =0时,OP=OQ;
=0时,OP=OQ; .
.| A.①② | B.②③ | C.①③ | D.①④ |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 的图象上,且x1<x2<0<x3.则y1、y2、y3的大小关系为 ( )
的图象上,且x1<x2<0<x3.则y1、y2、y3的大小关系为 ( )| A.y1<y2<y3 | B.yl>y2>y3 | C.y2>y3>yl | D.y2>y1>y3 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
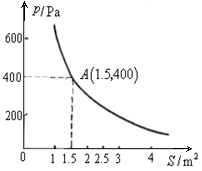
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com