
【题目】如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.
(1)求证:△ABQ≌△CAP;
(2)当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.
(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,直接写出它的度数.

【答案】(1)证明见解析;(2)点P、Q在运动的过程中,∠QMC不变.理由见解析.(3)不变,理由见解析.
【解析】试题分析:(1)、根据等边三角形可得∠ABQ=∠CAP,AB=CA,根据速度相同可得AP=BQ,从而得出三角形全等;(2)、根据△ABQ≌△CAP得出∠BAQ=∠ACP,然后根据∠QMC=∠BAQ+∠MAC得出答案;(3)、根据△ABQ≌△CAP得出∠BAQ=∠ACP,然后根据∠QMC=∠BAQ+∠MAC得出答案.
试题解析:(1)、∵△ABC是等边三角形 ∴∠ABQ=∠CAP,AB=CA, 又∵点P、Q运动速度相同,
∴AP=BQ, 在△ABQ与△CAP中,AB=AC,∠ABQ=∠CAP,AP=BQ ∴△ABQ≌△CAP(SAS);
(2)、点P、Q在运动的过程中,∠QMC不变.
理由:∵△ABQ≌△CAP, ∴∠BAQ=∠ACP, ∵∠QMC=∠ACP+∠MAC, ∴∠QMC=∠BAQ+∠MAC=∠BAC=60°
(3)、点P、Q在运动到终点后继续在射线AB、BC上运动时,∠QMC不变.
理由:∵△ABQ≌△CAP, ∴∠BAQ=∠ACP, ∵∠QMC=∠BAQ+∠APM,
∴∠QMC=∠ACP+∠APM=180°-∠PAC=180°-60°=120°


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
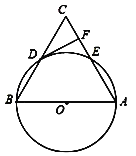
【题目】如图,在△ABC中,以AB为直径的⊙O分别与BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,求![]() 的长(结果保留π).
的长(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算2x(9x2-3ax+a2)+a(6x2-2ax+a2)等于( )
A. 18x3-a3 B. 18x3+a3 C. 18x3+4ax2 D. 18x3+3a3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现在的青少年由于沉迷电视、手机、网络游戏等,视力日渐减退,我市为了解学生的视力变化情况,从全市八年级随机抽取了1200名学生,统计了每个人连续三年视力检查的结果,根据视力在4.9以下的人数变化制成折线统计图,并对视力下降的主要因素进行调查,制成扇形统计图.

解答下列问题:
(1)图中“其他”所在扇形的圆心角度数为 ;
(2)若2016年全市八年级学生共有24000名,请你估计视力在4.9以下的学生约有多少名?
(3)根据扇形统计图信息,你认为造成中学生视力下降最主要的因素是什么,你觉得中学生应该如何保护视力?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com