
【题目】如图,已知点![]() ,
,![]() 分别是
分别是![]() 的边
的边![]() 和
和![]() 延长线上的点,作
延长线上的点,作![]() 的平分线
的平分线![]() ,若
,若![]() .
.
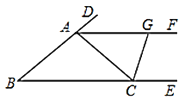
(1)求证:![]() 是等腰三角形;
是等腰三角形;
(2)作![]() 的平分线交
的平分线交![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的度数.
的度数.
【答案】(1)证明过程见解析;(2)70°
【解析】
(1)根据角平分线的性质得到∠DAF=∠FAC,再结合平行线的性质即可得出答案;
(2)根据角平分线的相知得出∠ACG=∠GCE,再根据等腰三角形的性质得出∠BCA和∠ACG,最后结合平行线的性质即可得出答案.
(1)证明:∵AF是∠DAC的角平分线
∴∠DAF=∠FAC
又AF∥BC
∴∠FAC=∠ACB,∠DAF=∠B
∴∠ACB=∠B
∴△ABC是等腰三角形
(2)解:∵CG平分∠ACE
∴∠ACG=∠GCE
又∠B=40°,△ABC是等腰三角形
∴∠BCA =40°
∴∠ACE=180°-∠BCA=140°
∠ACG=∠GCE=![]() ∠ACE=70°
∠ACE=70°
∴∠BCG=∠BCA+∠ACG=110°
又AF∥BC
∴∠AGC=180°-∠BCG=70°


科目:初中数学 来源: 题型:
【题目】如图,△ACE是以平行四边行ABCD的对角线AC为边的等边三角形,点C与点E关于x轴对称.若E点的坐标是(10,-4![]() ),则D点的坐标是( )
),则D点的坐标是( )

A.(6,0)B.(6![]() ,0)C.(8,0)D.(8
,0)C.(8,0)D.(8![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() 与x轴交于A,B两点(A在B的左侧),与y轴交于点C,顶点为D.
与x轴交于A,B两点(A在B的左侧),与y轴交于点C,顶点为D.
(1)请直接写出点A,C,D的坐标;
(2)如图(1),在x轴上找一点E,使得△CDE的周长最小,求点E的坐标;
(3)如图(2),F为直线AC上的动点,在抛物线上是否存在点P,使得△AFP为等腰直角三角形?若存在,求出点P的坐标,若不存在,请说明理由.
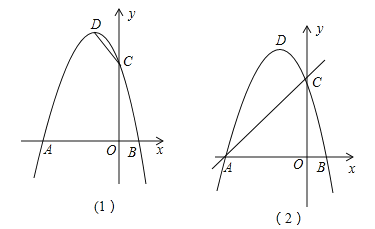
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0).下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④3a+c=0;则其中说法正确的是( ).

A. ①② B. ②③ C. ①②④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
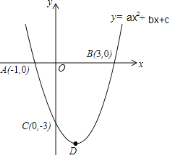
【题目】已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 和点
和点![]() 的坐标分别为
的坐标分别为![]() ,抛物线的对称轴为
,抛物线的对称轴为![]() ,
,![]() 为抛物线的顶点.
为抛物线的顶点.
![]() 求抛物线的解析式.
求抛物线的解析式.
![]() 抛物线的对称轴上是否存在一点
抛物线的对称轴上是否存在一点![]() ,使
,使![]() 为等腰三角形?若存在,写出点
为等腰三角形?若存在,写出点![]() 点的坐标,若不存在,说明理由.
点的坐标,若不存在,说明理由.
![]() 点
点![]() 为线段
为线段![]() 上一动点,过点
上一动点,过点![]() 作
作![]() 轴的垂线,与抛物线交于点
轴的垂线,与抛物线交于点![]() ,求四边形
,求四边形![]() 面积的最大值,以及此时点
面积的最大值,以及此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() (k>0)与矩形OABC在第一象限相交于D、E两点,OA=2,OC=4,连接OD、OE、DE.记△OAD、△OCE的面积分别为S、S .
(k>0)与矩形OABC在第一象限相交于D、E两点,OA=2,OC=4,连接OD、OE、DE.记△OAD、△OCE的面积分别为S、S .
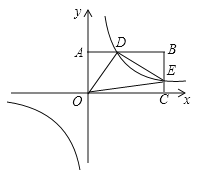
(1)①点B的坐标为 ;②S S(填“>”、“<”、“=”);
(2)当点D为线段AB的中点时,求k的值及点E的坐标;
(3)当S+S=2时,试判断△ODE的形状,并求△ODE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分10分 )在端午节前夕三位同学到某超市调研一种进价为2元的粽子的售销情况,请跟据小丽提供的信息,解答小华和小明提出的问题
小丽:每个定价3元,每天能卖出500个,而且,这种粽子每上涨0.1元,其售销量将减小10个
小华:照你所说,如果实现每天800元的售销利润,那该如何定价?莫忘了物价局规定售价不能超过进价的240%哟
小明:800元售销利润是不是最多的呢?如果不是,那该如何定价,才会使每天的利润最大?.
(1)小华的问题解答:
(2)小明的问题解答:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com