
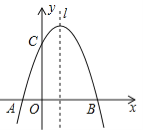
【题目】如图,已知抛物线![]() 与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0)
与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0)
(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.
科目:初中数学 来源: 题型:
【题目】为保障我国海外维和部队官兵的生活,现需通过A港口、B港口分别运送100吨和50吨生活物资.已知该物资在甲仓库存有80吨,乙仓库存有70吨,若从甲、乙两仓库运送物资到港口的费用(元/吨)如表所示:

(1)设从甲仓库运送到A港口的物资为x吨,求总运费y(元)与x(吨)之间的函数关系式,并写出x的取值范围;
(2)求出最低费用,并说明费用最低时的调配方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a、b、c为常数,a≠0)经过点A(﹣1,0),B(5,﹣6),C(6,0).
(a、b、c为常数,a≠0)经过点A(﹣1,0),B(5,﹣6),C(6,0).
(1)求抛物线的解析式;
(2)如图,在直线AB下方的抛物线上是否存在点P使四边形PACB的面积最大?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点Q为抛物线的对称轴上的一个动点,试指出△QAB为等腰三角形的点Q一共有几个?并请求出其中某一个点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
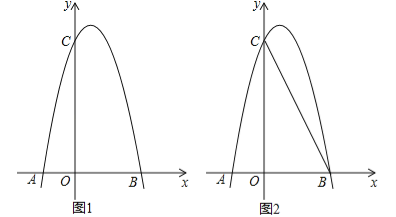
【题目】如图1,对称轴为直线x=![]() 的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A.
的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A.
(1)求抛物线的解析式;
(2)若点P为第一象限内抛物线上的一点,设四边形COBP的面积为S,求S的最大值;
(3)如图2,若M是线段BC上一动点,在x轴是否存在这样的点Q,使△MQC为等腰三角形且△MQB为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
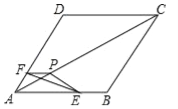
【题目】如图,把△EFP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF=![]() ,∠BAD=60°,且AB>
,∠BAD=60°,且AB>![]() .
.
(1)求∠EPF的大小;
(2)若AP=10,求AE+AF的值;
(3)若△EFP的三个顶点E、F、P分别在线段AB、AD、AC上运动,请直接写出AP长的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细阅读下面例题,解答问题;
例题,已知二次三项式x2﹣4x+m有一个因式是(x+3),求另一个因式以及m的值.
解:设另一个因式为(x+n),得x2﹣4x+m=(x+3)(x+n)
则x2﹣4x+m=x2+(n+3)x+3n
∴ ![]()
解得:n=﹣7,m=﹣21
∴另一个因式为(x﹣7),m的值为﹣21
问题:仿照以上方法解答下面问题:
已知二次三项式3x2+5x﹣m有一个因式是(3x﹣1),求另一个因式以及m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com