Question

已知∠MAN=135°，正方形ABCD绕点A旋转．

（1）当正方形ABCD旋转到∠MAN的外部（顶点A除外）时，AM，AN分别与正方形ABCD的边CB，CD的延长线交于点M，N，连接MN．

①如图1，若BM=DN，则线段MN与BM+DN之间的数量关系是　MN=BM+DN　；

②如图2，若BM≠DN，请判断①中的数量关系是否仍成立？若成立，请给予证明；若不成立，请说明理由；

（2）如图3，当正方形ABCD旋转到∠MAN的内部（顶点A除外）时，AM，AN分别与直线BD交于点M，N，探究：以线段BM，MN，DN的长度为三边长的三角形是何种三角形，并说明理由．

Answer 1

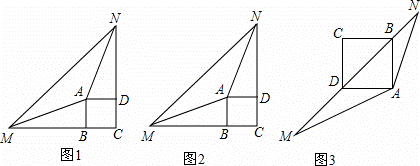
解：（1）①如图1，若BM=DN，则线段MN与BM+DN之间的数量关系是MN=BM+DN．理由如下：

在△ADN与△ABM中，

，

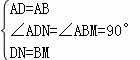∴△ADN≌△ABM（SAS），

∴AN=AM，∠NAD=∠MAB，

∵∠MAN=135°，∠BAD=90°，

∴∠NAD=∠MAB=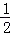（360°﹣135°﹣90°）=67.5°，

作AE⊥MN于E，则MN=2NE，∠NAE=∠MAN=67.5°．

在△ADN与△AEN中，

，

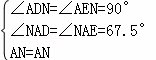∴△ADN≌△AEN（AAS），

∴DN=EN，

∵BM=DN，MN=2EN，

∴MN=BM+DN．

故答案为MN=BM+DN；

②如图2，若BM≠DN，①中的数量关系仍成立．理由如下：

延长NC到点P，使DP=BM，连结AP．

∵四边形ABCD是正方形，

∴AB=AD，∠ABM=∠ADC=90°．

在△ABM与△ADP中，

，

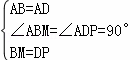∴△ABM≌△ADP（SAS），

∴AM=AP，∠1=∠2=∠3，

∵∠1+∠4=90°，

∴∠3+∠4=90°，

∵∠MAN=135°，

∴∠PAN=360°﹣∠MAN﹣（∠3+∠4）=360°﹣135°﹣90°=135°．

在△ANM与△ANP中，

，

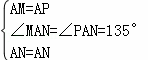∴△ANM≌△ANP（SAS），

∴MN=PN，

∵PN=DP+DN=BM+DN，

∴MN=BM+DN；

（2）如图3，以线段BM，MN，DN的长度为三边长的三角形是直角三角形．理由如下：

∵四边形ABCD是正方形，

∴∠BDA=∠DBA=45°，

∴∠MDA=∠NBA=135°．

∵∠1+∠2=45°，∠2+∠3=45°，

∴∠1=∠3．

在△ANB与△MAD中，

，

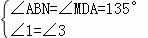∴△ANB∽△MAD，

∴=，

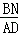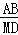∴AB²=BN•MD，

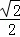∵AB=DB，

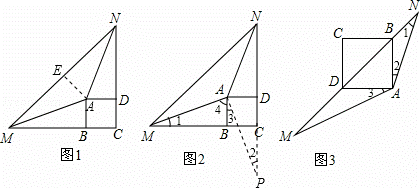
∴BN•MD=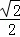（DB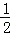）²=BD²，

∴BD²=2BN•MD，

∴MD²+2MD•BD+BD²+BD²+2BD•BN+BN²=MD²+BD²+BN²+2MD•BD+2BD•BN+2BN•MD，

∴（MD+BD）²+（BD+BN）²=（DM+BD+BN）²，

即MB²+DN²=MN²，

∴以线段BM，MN，DN的长度为三边长的三角形是直角三角形．