
| A. | -$\frac{2}{5}$ | B. | -$\frac{2}{9}$ | C. | -$\frac{4}{7}$ | D. | -$\frac{2}{7}$ |
分析 首先根据四边形ABCD的四个顶点的坐标,判断出四边形ABCD是平行四边形,然后根据过平行四边形中心的直线把平行四边形分成面积相等的两部分,再根据直线y=kx+2经过四边形ABCD的顶点C,判断出直线y=kx+2是BC所在的直线,据此求出k的值为多少即可.
解答 解:如图1,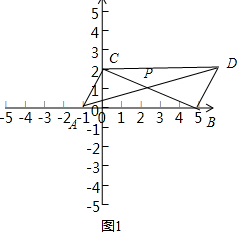
∵A(-1,0),B(5,0),C(6,2),D(0,2),
∴AB=5-(-1)=6,CD=6-0=6,
又∵点C、D的纵坐标相同,
∴AB∥CD且AB=CD,
∴四边形ABCD是平行四边形,
∵当x=0时,y=k×0+2=2,
∴直线y=kx+2经过四边形ABCD的顶点C,
又∵直线y=kx+2将四边形ABCD分成面积相等的两部分,
∴直线y=kx+2是BC所在的直线,
∴k=$\frac{2-0}{0-5}=-\frac{2}{5}$.
故选:A.
点评 此题主要考查了一次函数的性质的应用,以及平行四边形的判定和性质的应用,要熟练掌握,解答此题的关键是判断出直线y=kx+2是BC所在的直线.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 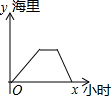 | B. | 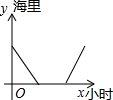 | C. |  | D. | 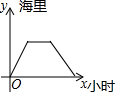 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | 0 | C. | -1 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了弘扬“社会主义核心价值观”,市政府在广场树立公益广告牌,如图所示,为固定广告牌,在两侧加固钢缆,已知钢缆底端D距广告牌立柱距离CD为3米,从D点测得广告牌顶端A点和底端B点的仰角分别是60°和45°.
为了弘扬“社会主义核心价值观”,市政府在广场树立公益广告牌,如图所示,为固定广告牌,在两侧加固钢缆,已知钢缆底端D距广告牌立柱距离CD为3米,从D点测得广告牌顶端A点和底端B点的仰角分别是60°和45°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com